Reverse Sprinkler
April 8, 2024
 Eric Sevareid (1912-1992)
Eric Sevareid (1912-1992) was a prominent
journalist and
World War II correspondent who made the transition from
print media to
television in its early years. Sevareid was
hired by
Edward R. Murrow (1908-1965) as a member of the
CBS News team, and he served as a
commentator on the
CBS Evening News for thirteen years.
Wikimedia Commons image
I
remember one of Sevareid's commentaries on the CBS Evening News with
Walter Cronkite (1916-2009). He contrasted
photographs of
smiling diplomats in the
1970s with the
austere photos earlier in the
20th century. He said that this wasn't because the
world was a better place in the 1970's, but that
statesmen early in the century all had
rotten teeth. I was reminded of this during a recent visit to my
dentist, at which we also discussed the
physics of
oral irrigators, a.k.a., Waterpiks.
In that conversation I somehow remembered
Bernoulli's principle, named after
Swiss physicist,
Daniel Bernoulli (1700-1782). According to Bernoulli's principle, the
velocity of a
fluid increases as the
diameter of a
pipe decreases. For an
incompressible fluid, the fluid velocity
v1 changes to a new velocity
v2 in
proportion to the
ratio of the pipe
cross-sectional areas A1 and
A2,
v2 = v1(A1/A2)
My Waterpik is not the only example of
hydraulics in my
house. We get our
water from a
well that's 75 feet
deep with the
water pump at the bottom, rather than in our house. The reason for this is that an ideal pump producing a perfect
vacuum can only lift water 33.9
feet. We can't
suck the water from the well; so, we need to pump it out.
Piston pumps in the
16th century were only capable of sucking water to a height of about 24 feet. As described in Book VI of
De re metallica (On the Nature of Metals) by
Georgius Agricola (1494-1555),
miners would suck water from their
mines using a
cascade of pumps to lift water to one level, and then upwards to another. As he writes,

"Because these pumps can only lift water about 24 feet, batteries of pumps are required for the deepest mines. It is composed of several pumps, which do not, like those last described, go down into the
shaft together, but of which one is below the other, for if there are three, as is generally the case, the lower one lifts the water of the
sump and pours it out into the first tank; the second pump lifts again from that tank into a second tank, and the third pump lifts it into the
drain of the
tunnel."[1]
(Project Gutenberg image.[1])
Another common household hydraulic device is the
lawn sprinkler. Most of these in use today have a
mechanism that
sprays water in an overhead
arc or in a
radial pattern to ensure coverage of a large area. The simplest, but less
effective, type of lawn sprinkler is the one that uses the
force of water
jets to propel a radial spray. This type of lawn sprinkler was described a hundred and fifty years ago in the 1883 physics
textbook,
The Science of Mechanic by
Austrian physicist,
Ernst Mach (1838-1916) (see figure).[2]
Albert Einstein (1879-1955) was influenced by Mach's
concept of
inertia. The fundamental
idea of this device, using
steam instead of water, was described by
Greek mathematician and
engineer,
Hero of Alexandria (fl. 60 AD), in his book,
Pneumatica. I wrote about this device, called an
Aeolipile, in a
previous article (Steam Power, January 28, 2011).
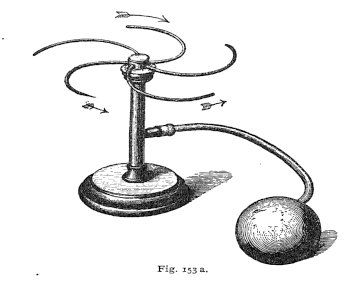
Figure 153a from the Science of Mechanics (1883) by Ernst Mach. This is an air propelled version of a lawn sprinkler.
Mach, who was an accomplished experimental physicist, is famous also for the eponymous theoretical principle known as Mach's principle.
The ancients would reference things to the "fixed stars," and this same idea is behind Mach's principle that a local spinning object has centrifugal force because of its spin relative to all the other matter in the universe.
(Figure from ref. 2.[2] Click for larger image.)
The device in the above figure, an
air propelled version of a
lawn sprinkler, will
rotate when the attached
rubber bulb is
pressed. Mach noted that when the rubber bulb is released, sucking air, the device showed "no distinct rotation," a clear demonstration of
time-reversal asymmetry.[2]
Nobel Physics Laureate,
Richard Feynmen (1918-1988), became interested in the reverse sprinkler when he was a
graduate student at
Princeton University, and he mentioned it in his
autobiography,
Surely You're Joking, Mr. Feynman!.[3] The problem has since been called the
Feynman sprinkler. Some
experiments using low
friction spinners and high external fluid
pressures resulting in high
inflow rates have shown a reverse spin. However the mechanism that causes the reverse spin was elusive.
As is often the case, one simple experiment is worth more than a hundred
theoretical papers. A recent experiment by scientists from
New York University (New York, New York) and the
Colorado School of Mines (Golden, Colorado) elucidated the mechanism of the reverse sprinkler.[4-7] They used a sprinkler with an ultra-low-friction rotary
bearing immersed in water containing
dyed microparticles illuminated by a
laser to track the fluid flow on high-speed
video.[4-7] The reverse sprinkler's rotation was fifty times slower than that of a forward sprinkler, and the reverse motion was the result of an asymmetry in the inward flowing water jets caused by the rotation of the sprinkler, a consequence of the water's being forced outward by centrifugal force.[5-7]

Flow pattern of a reverse sprinkler, as revealed by laser illuminated microparticles. For this visualization, movement of the device was prevented. A complex flow is seen internal to the sprinkler. (Still image from an NYU Applied Mathematics Laboratory video. Click for larger image.)
Previous reverse sprinkler experiments have shown mixed results, some demonstrating steady rotation, some just transient rotation, and others having an
oscillating rotation direction.[7] Knowing that the friction forces acting on the sprinkler would greatly affect its rotation, the research team designed a sprinkler head that
floats freely when immersed in water.[5-6] Rotational forces that allowed both normal and reverse rotation were achieved by adjusting a connected
siphon tube from the center of the sprinkler to a side
tank.[5] The
transparent sprinkler head allowed observation of details of the water flow both internal and external to the sprinkler.[7]
The experiments found that the reverse flow case is not a time-reversed version of normal flow.[5] The
torque required for the reverse rotation arises from an asymmetry in the direction of the inward water jets caused by the rotation itself.[5] The researchers developed a
mathematical model of the flow patterns that explains the observations.[4-5] This research was
funded by the
National Science Foundation.
References:
- Georgius Agricola, "De Re Metallica," First Latin Edition of 1556, Herbert Clark Hoover and Lou Henry Hoover, Trans., Dover Publications, 1950
- Ernst Mach, "The Science of Mechanics. T. J. McCormack, Trans., Open Court Publishing (Chicago, 1919), 534 pp..
- Richard P. Feynman and Ralph Leighton, "Surely You're Joking, Mr. Feynman!": Adventures of a Curious Character, W. W. Norton & Company; Reissue edition (February 6, 2018), Paperback, 400 pp., ISBN: 978-0393355628 (via Amazon).
- Kaizhe Wang, Brennan Sprinkle, Mingxuan Zuo, and Leif Ristroph, "Centrifugal Flows Drive Reverse Rotation of Feynman's Sprinkler," Phys. Rev. Lett., vol. 132, no. 4 (January 26, 2024), Article no. 044003, DOI:https://doi.org/10.1103/PhysRevLett.132.044003.
- Philip Ball, " Feynman's Reversed Sprinkler Puzzle Solved," Physics, vol. 17, no. 15 (January 26, 2024).
- How does a "reverse sprinkler" work? Researchers solve decades-old physics puzzle, New York University Press Release, January 29, 2024.
- Jennifer Ouellette, "A decades-old conundrum - Mathematicians finally solved Feynman’s "reverse sprinkler" problem," Ars Technica, February 2, 2024.
Linked Keywords: Eric Sevareid (1912-1992); journalist; World War II; correspondent; print; mass media; television; employment; hired; Edward R. Murrow (1908-1965); CBS News; commentator; CBS Evening News; Wikimedia Commons; memory; remember; Walter Cronkite (1916-2009); photograph; smile; smiling; diplomat; 1970s; austere; 20th century; world; statesmen; tooth decay; rotten teeth; dentist; physics; oral irrigator; Bernoulli's principle; Swiss; physicist; Daniel Bernoulli (1700-1782); velocity; fluid; diameter; pipe (fluid conveyance); compressibility; incompressible; proportionality (mathematics); proportion; ratio; cross section (geometry); cross-sectional; area; hydraulics; house; water; well; depth (coordinate); pump; vacuum; foot (unit); feet; suction; suck; piston pump; 16th century; De re metallica (On the Nature of Metals); Georgius Agricola (1494-1555); miner; mining; mine; cascade; shaft (civil engineering); sump; drain (plumbing); tunnel; Project Gutenberg; irrigation sprinkler; lawn sprinkler; mechanism (engineering); sprayer; spray; arc (geometry); radius; radial; pattern; efficiency; effective; force; jet (fluid); textbook; Austria; Austrian; Ernst Mach (1838-1916); Albert Einstein (1879-1955); conceptual model; concept; inertia; idea; steam; Greek; mathematician<; engineer; Hero of Alexandria (fl. 60 AD); The Science of Mechanics (1883); atmosphere of Earth; air; propulsion; propelled; experimental physics; experimental physicist; celebrity; famous; eponym; eponymous; theory; theoretical; physical law; principle; Mach's principle; Ancient Greece; ancients; reference; fixed stars; angular momentum; spinning; centrifugal force; matter; universe; rotation; rotate; rubber bulb; compression (physical); press; T-symmetry; time-reversal; asymmetry; Nobel Physics Laureate; Richard Feynmen (1918-1988); postgraduate education; graduate student; Princeton University; autobiography; Feynman sprinkler; experiment; friction; pressure; fluid dynamics; inflow; rate (mathematics); scientific literature; paper; New York University (New York, New York); Colorado School of Mines (Golden, Colorado); elucidate; elucidated; bearing (mechanical); dye; dyed; microparticle; lighting; illuminated; laser; video; flow pattern of a reverse sprinkler; scientific visualization; NYU Applied Mathematics Laboratory; oscillation; oscillating; buoyancy; float; siphon; tube (fluid conveyance); storage tank; transparency; transparent; torque; mathematical model; funding of science; funded; National Science Foundation.