The Birthday Problem
September 25, 2023
Prior to starting a mathematical
mathematical proof, it's important to check the
veracity of your
axioms. Axioms are
concepts that are so evident that they are accepted without question.
Geometrical axioms were called
postulates in
Euclid's Elements, and postulates in
The Elements are such things as the ability to draw a
straight line between any two
points. Euclid's fifth postulate, also known as the
parallel postulate, admits the
possibility of
parallel,
non-intersecting lines. While this is true for the
two-dimensional space of Euclidian geometry, it isn't true for
curved surfaces such as the
surface of a sphere. For that reason, a
triangle drawn on the surface of a sphere has a sum of
interior angles that's greater than 180
degrees.

Euclid's fifth postulate, the parallel postulate, Book 1, Definition 23, of his Elements.
The English translation reads, "Parallel lines are straight lines which, being in the same plane, and being produced to infinity in each direction, meet with one another in neither (of these directions)."[1]
Greek text and English translation from ref. 1.[1] The background is derived from the Wikimedia Commons image of an early 9th century manuscript.
I was reminded of the importance of axioms by an experience that one of my
grandsons had at a
birthday party. Among the party
treats were
bags of
M&M's candies. These
chocolate candies have a thin
coating colored red, orange, yellow, green, blue, and brown. He found that there were ten yellow pieces in one of his M&M's bags having twelve pieces.
If our axiom is that there's a
uniform distribution of colors
manufactured, the
probability of getting at least ten yellow candies would be (1/6)
10 = 1.65382x10
-8, and the probability of getting exactly ten yellow candies would be (1/6)
10·(5/6)
2 = 1.14848x10
-8.
While it's known that the color distribution
deviates somewhat from uniformity,[2] there's obviously something about the
manufacturing process, such as non-uniform
mixing, that's happened.
Wikimedia Commons image by Evan-Amos of the Vanamo Online Game Museum
Also related to birthdays is a probability problem known as the
birthday problem. This problem is to determine the probability that at least two people in a group of
N people will share a birthday.[3] This is different from the probability that another person in the group will share your birthday, which is simply
N/365, if we exclude
leap year birthdays. Relaxing the requirement of matching a specific
date to the condition that any two people will have matching birthdays gives the interesting result that
N = 23 gives better than a 50:50 chance for a match.[3] This is a
consequence of there being so many pairs,
N x (N-1)/2 pairs, which is 253 for
N = 23 people.
There's a simple
permutation equation for
calculating the probability for any
N. However, there's much more
fun in doing a
Monte Carlo simulation. I generally use
PHP for simple simulations such as this, and I've released the PHP
source code in
this zip file. The following
graph shows the probability of a shared birthday among a group of
N people. The calculated value at
N =23 is 0.5087. The table shows the probability for various values of
N.
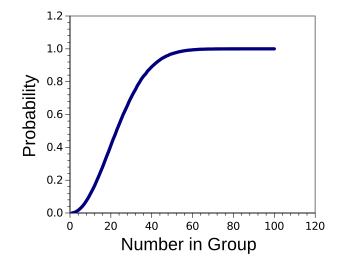
Graph of birthday problem probabilities.
(Graphed using Gnumeric from data generated by my simulation program.
The birthday problem has a practical use. In
cryptanalysis, the
birthday attack reduces the computation needed in finding
hash collisions.
I decided to investigate another birthday problem, this one involving
thermodynamics, rather than mathematics. This is the question of how long a birthday
candle will
burn. The first figure below shows two types of birthday candles, a smaller one for
cupcakes, and a larger one for a large
cake. The second figure shows the
flame sizes of the two birthday candles, along with a
dinner table candle for
reference.

Two sizes of birthday candles. The upper candle is a larger size for cakes, and the lower is a smaller size for cupcakes. (Photo by the author.)

A composite image of candle flames at the same scale. Leftmost is a large dinner table candle. Center is a large birthday candle for a cake. Right is a small birthday candle for a cupcake. Surprisingly, the flame size does not scale with candle size.
According to a study by the US National Institute of Standards and Technology (NIST), "the burning rate and heat flux from the candle flame depends on many interdependent factors including wick length, wick shape, mass burning rate, heat release rate, flame height, and paraffin wax formulation..."[4]
(Photo by the author.)
Paraffin wax, a
mixture of
hydrocarbon molecules containing between 20 and 40
carbon atoms, is generally used as a candle
material. The
US National Institute of Standards and Technology (NIST) found that the
heat of combustion (Hc) of a paraffin wax candle is about 43.8
kJ/
g, and its heat release rate was 77 ± 9
W.[4] My large birthday candle had a mass of 2.75 g, and my small birthday candle had a mass of 1.0 g. This leads to the
lifetime calculation in the following table.
Calculated Birthday Candle Lifetime
| Quantity |
Small Candle |
Large Candle |
| Mass (g) |
1.00 |
2.75 |
| Hc(kJ/g) |
43.8 |
43.8 |
| Total Energy Released (J) |
43,800 |
120,450 |
| Energy Release Rate (W) |
77 ± 9 |
77 ± 9 |
| Lifetime (sec) |
509-644 |
1401-1771 |
| Lifetime (mm:ss) |
8:29-10:44 |
23:21-29:31 |
My own
observations indicate that these calculated lifetimes are somewhat longer than normally seen. Our axiom, that birthday candles are equivalent to the standard candles of the NIST study, is not true. There's an
online burn-time calculator for candles made from paraffin wax and other waxes.[5]
References:
- Book 1, definition 23, of Euclid's Elements of Geometry, Greek text of J.L. Heiberg (1883–1885) and modern English translation, by Richard Fitzpatrick, 2008, ISBN 978-0-6151-7984-1 (PDF File).
- Rick Wicklin, "The distribution of colors for plain M&M candies," SAS Blog, February 20, 2017.
- Science Buddies, "Probability and the Birthday Paradox," Scientific American, March 29, 2012.
- Anthony Hamins and Matthew Bundy, "Characterization of Candle Flames," Journal of Fire Protection Engineering, vol. 15, no. 4 (November 2005), pp. 265-285, https://doi.org/10.1177/1042391505053. A PDF file at the NIST Website.
- Candle Burn Time Calculator at rechneronline.de.
Linked Keywords: Mathematical proof; truth; veracity; axiom; concept; geometry; geometrical; postulate; Euclid's Elements; straight line; point (geometry); parallel postulate; existence; possibility; parallel (geometry); intersection (Euclidean geometry); non-intersecting; two-dimensional space; curvature; curved surface; spherical geometry; surface of a sphere; triangle; interior angle; degree (angle); Euclid; Euclidean geometry; English language; translation; plane (geometry); infinity; direction (geometry); Greek language; background; Wikimedia Commons; 9th century; manuscript; grandchild; grandson; birthday; party; snack; treat; food packaging; bag; M&M's candies; chocolate; candy; candies; coating; color; uniform distribution; manufacturing; manufactured; probability; deviation (statistics); deviate; process (engineering); mixing (process engineering); Evan-Amos of the Vanamo Online Game Museum; birthday problem; leap year; calendar date; logical consequence; permutation; equation; calculation; calculating; entertainment; fun; Monte Carlo simulation; PHP; source code; birthday simulation.zip; Cartesian coordinate system; graph; Gnumeric; cryptanalysis; birthday attack; hash collision; thermodynamics; candle; combustion; burn; cupcake; cake; flame; dinner table; standard (metrology); reference; photomontage; composite image; scale (ratio); research; study; US National Institute of Standards and Technology (NIST); reaction rate; heat flux; interdependent factor; candle wick; length; geometry; shape; mass; combustion; burning; reaction rate; heat transfer; heat release; height; paraffin wax; formulation; mixture; hydrocarbon; molecules; carbon; atom; material; heat of combustion (Hc); kilojoule (kJ); gram (g); Watt (W); service life; lifetime; observation; Internet; online.