Phase Rule
November 9, 2020
Algebra was the
mathematics taught during the first year of
high school in
my era, and it was one
equation after another. The mathematics taught during the next year,
Euclidean geometry (called
plane geometry), was devoid of equations. Perhaps the lack of equations was the reason it was more enjoyable to me. Later, I started a
course in
solid geometry. This was far less enjoyable, since I disliked the
teacher. Since it was not a required course, I dropped-out. If I had continued, I might have been introduced to the first important geometry equation,
Euler's polyhedron formula.
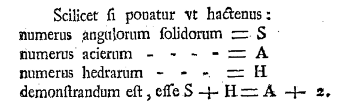
Euler's polyhedron formula, as written in his 1758 paper, "Elementa doctrinae solidorum" (Elements of the doctrine of solids).
The hardest part in reading this (apart from the Latin) is to remember that what looks like an "f" is actually an "s." In Euler's notation, A is the number of edges, H is the number of faces, and S is the number of vertices ("solid angles"). (Via the Scholarly Commons at the University of the Pacific.[1] Click for larger image.)
This equation was first stated in 1758 by preeminent
mathematician,
Leonhard Euler (1707-1783). It describes a property of
convex polyhedra based on the number of their
faces (
F),
edges (
E), and
vertices (
V).
V - E + F = 2
This is demonstrated for the
Platonic solids in the following table.
Euler gave a
proof for the validity of this equation; but, just as for the
Pythagorean theorem, for which at least 370 unique proofs are known, many more have followed. One
website gives twenty proofs of Euler's polyhedron formula.[2]
Vertices seem to have a special role, since faces are always joined by one edge, edges join two faces, but vertices are common to a varied number of edges and faces.
Thermodynamics has its own version of the vertex in the
triple point, the point on the
pressure-
temperature phase diagram of a
material at which the
solid,
liquid and
gas phases coexist in
thermodynamic equilibrium.
The
triple point of water occurs at 273.1575
K (0.0075
°C, 32.0135
°F) and a
partial pressure of
water vapor of 6.11657
mbar. Although the pressure is much below
atmospheric pressure, what's important here is the partial pressure of water; and, since the
slope of the solid-liquid
phase boundary is steep, the temperature is not that removed from what's considered to be the
melting point of
ice.
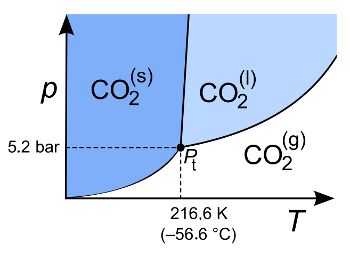
Triple point of carbon dioxide in its pressure-temperature phase diagram.
You will only see liquid CO2 at very high pressures. That's why there's a transition from solid to gas (sublimation) at standard laboratory conditions.
(Wikimedia Commons image by Sponk (Modified). Click for larger image.)
The thermodynamics of phase equilibrium, as for the triple point, are summarized in the
phase rule, derived by eminent
thermodynamicist,
J. Willard Gibbs (1839-1903), around 1875. Gibbs created
statistical mechanics, which explains the
laws of thermodynamics in terms of the
statistical properties of
ensembles of
particles. This phase rule equation, reminiscent of Euler's polyhedron formula, is as follows:
F = C - P + 2
In this equation,
F is the number of
degrees of freedom of the
system,
C is the number of its components, and
P is the number of phases. If we consider the triple point of a
pure substance (
C=1), we know that a
point has zero degrees of freedom, so we get
0 = 1 -P +2
P = 3
Although
Einstein apparently said that Gibbs' thermodynamics was the only
theory he really trusted,
researchers from the
Eindhoven University of Technology and the
University Paris-Saclay have discovered a system that demonstrates a five-phase equilibrium, contrary to the Gibbs' phase rule.[3-4] The system contains an
isotropic fluid,
nematic and
smectic liquid crystals, and two solid phases.[3]
It was found that this system has conditions for which four phases exist at the same time, and a point at which there are five coexisting phases.[4] This quintuple point has a gas phase, two liquid crystal phases, and two solid phases existing simultaneously.[4] Study author,
Mark Vis, an
assistant professor at Eindhoven, reports that "this is the first time that the famous Gibbs rule has been broken."[4]
As often happens in
research, this
phenomenon was discovered
accidentally,[4] in a manner reminiscent of
Dan Shechtman's discovery of
quasicrystals of supposedly
impossible five-fold symmetry. Two Eindhoven
graduate students, Álvaro González García and Vincent Peters saw an
impossible four-phase equilibrium in
computer simulations of
plate-shaped particles and a
polymer.[4] Further simulations with multiple shapes, such as cubes and also
rods showed the same effect.[4] Says
Remco Tuinier, a
professor at Eindhoven,
"With the rods, most phases turned out to be possible, we even found a five-phase equilibrium. That could also mean that even more complicated equilibria are possible, as long as you search long enough for complex different particle shapes."[4]
Why does this material system violate the Gibbs phase rule? Gibbs'
analysis did not include the shape of particles in the
mixture. Liquid crystals were discovered about a
decade after Gibbs derived the phase rule, and they were only understood much later. The study
authors have shown that the
ratio of particle
length to
diameter, and the diameter of particles in relation to the diameter of other particles in the
colloid-polymer mixture are as important as temperature and pressure.[3-4]

A five-phase thermodynamic equilibrium. Starting from the top, a gas phase with unaligned rods (isotropic phase), then a liquid phase with rods pointing in about the same direction (nematic liquid crystal), then a liquid phase with rods aligned in different layers (smectic-phase liquid crystal), and two solid phases at the bottom.[4]
One factor leading to this configuration is an excluded volume effect in which rods are pushed towards each other by polymer chains.[4]
(ICMS animation studio image. Click for larger image.)
As there any uses for this discovered affect? Many products, such as
mayonnaise and
paint, which are colloidal mixtures, and
liquid crystal displays, use similar materials.[4] Says Vis, "Most
industries choose to work with a single-phase system, where there is no
segregation. But if the exact
transitions are clearly described, then the industry can actually use those different phases instead of avoiding them."[4]
References:
- Leonhard Euler, Elementa doctrinae solidorum (Elements of the doctrine of solids), Novi Commentarii academiae scientiarum Petropolitanae, vol. 4 (1758), pp. 109-140, Enestrom No. 230, via Scholarly Commons at the University of the Pacific.
- XX
Twenty Proofs of Euler's Formula: V-E+F=2, The Geometry Junkyard
David Eppstein, Theory Group, Donald Bren School of Information and Computer Sciences, UC Irvine.
- V. F. D. Peters, M. Vis, Á. Gonz´lez García, H. H. Wensink, and R. Tuinier, "Defying the Gibbs Phase Rule: Evidence for an Entropy-Driven Quintuple Point in Colloid-Polymer Mixtures, Phys. Rev. Lett., vol. 125, no. 12 (September 18, 2020), Article no. 127803, DOI:https://doi.org/10.1103/PhysRevLett.125.127803. This is an open access article with a PDF file here.
- Defying a 150-year-old rule for phase behavior, Eindhoven University of Technology Press Release, September 18, 2020.
Linked Keywords: Algebra; mathematics; high school; baby boomer; my era; equation; Euclidean geometry; plane (geometry); course (education); solid geometry; teacher; Euler characteristic; Euler's polyhedron formula; academic publishing; paper; reading; Latin; notation; edge (geometry); face (geometry); vertex (geometry); vertices; angle; Scholarly Commons at the University of the Pacific; mathematician; Leonhard Euler (1707-1783); convex polytope; convex polyhedrn; Platonic solid; Tetrahedron; Cube; Octahedron; Regular Dodecahedron; Regular Icosahedron; mathematical proof; Pythagorean theorem; website; thermodynamics; triple point; pressure; temperature; phase diagram; material; solid; liquid; gas; phase (matter); thermodynamic equilibrium; triple point of water; kelvin; K; Celsius; °C; Fahrenheit; °F; partial pressure; water vapor; bar (unit); mbar; atmospheric pressure; slope; phase boundary; melting point; ice; carbon dioxide triple point; carbon dioxide; pressure; temperature; phase diagram; high pressure; sublimation (phase transition); standard conditions for temperature and pressure; standard laboratory conditions; Wikimedia Commons; Sponk; phase rule; thermodynamicist; J. Willard Gibbs (1839-1903); statistical mechanics; laws of thermodynamics; statistical properties; statistical ensemble (mathematical physics); particle; degrees of freedom (physics and chemistry); physical system; pure substance; point (geometry); Albert Einstein; theory; research; researcher; Eindhoven University of Technology; Paris-Saclay University; University Paris-Saclay; isotropy; isotropic; fluid; Mark Vis; assistant professor; phenomenon; serendipity; accidentally; Dan Shechtman; quasicrystals; symmetry (physics); five-fold symmetry; postgraduate education; graduate student; computer simulation; plane (geometry); plate-shaped; polymer; cylinder (geometry); rod; Remco Tuinier; professor; analysis; mixture; decade; author; ratio; length; diameter; colloid; angle; unaligned; macromolecular crowding; excluded volume effect; polymer chain; ICMS animation studio; mayonnaise; paint; liquid crystal display; industry; segregation in materials; phase transition.