Weighing the Milky Way
May 13, 2019
Scientists usually take extreme care in the design and execution of their
experiments. The first
scientific conference that I attended had
chemical thermodynamics as its topic, and one of the sessions was on
calorimetry. One presenter had done
combustion calorimetry on some
volatile organic liquids contained in small
plastic pouches, so an
accurate weight of the
combusted materials was important to know. This
experimenter went a step further to correct for the
buoyancy of the entrapped
gas volume in the pouches during weighing, since the
vapor had a different
density than
air.
That may have been a step too far. "
The best is the enemy of the good" is one
aphorism that I've always followed. At times, extra effort leads to
diminishing returns. I was first introduced to this principle during
high school chemistry when I learned the concept of
significant figures in
calculating quantities of
reactants and their
products.
The same principle applies to the selection of
laboratory instrumentation. I've often used 5-1/2
digit benchtop multimeters (the "1/2" means that the maximum count is 199999), but it's rare when the 3-1/2 digit multimeter I purchased for about $20 doesn't give the information I need.
Digital pan balances with five or six digits are very convenient, but most of the weighing I've done in my
career didn't need such accuracy. Such was true throughout
history when simple
balance scales were used in
commerce and later in science.
The accurate measurement of
mass has been important to
humans since
antiquity, and balance scales with their associated balancing weights have existed for more than 4,000 years. The balance scale was so important to
human culture that it appears as the
constellation,
Libra, the
Latin word for the balance scale (see figure).
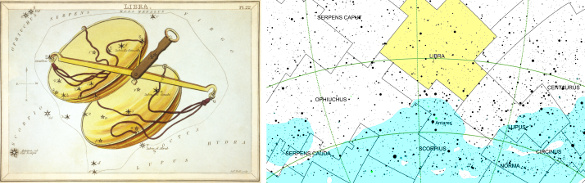
The constellation, Libra, as imagined in antiquity (left) and shown in yellow in a modern star chart near the Milky Way as rendered in light blue. The modern constellation boundaries are set by the International Astronomical Union (IAU). (Left image, "Libra," an illustration by Sidney Hall (1788–1831), plate 22 in Urania's Mirror (Jehoshaphat Aspin, London, 1825), United States Library of Congress digital ID cph.3g10068, via Wikimedia Commons. Right image from KStars. Click for larger image.)
The balance scale is a
conceptually simple way to measure mass, but how does one measure the mass of the
Earth? For that, some fundamental
physics is required in the form of the
law of universal gravitation, deduced by
Isaac Newton (1642-1727) and published in Book 1 (
De motu corporum), of his 1687
Philosophae Naturalis Principia Mathematica, known by the shorthand name
Principia. This law is simply stated,
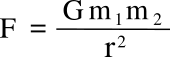
where
F is the
gravitational force between two masses,
m1 and
m2, and
r is the distance between them. We can obtain the mass of the Earth by measuring the force it exerts on a test mass, but only if we know the value of
G. The present
CODATA value of
G is 6.67408 x 10
-11 m3 kg-1 s-2, but it was first measured
experimentally by
British scientist,
Henry Cavendish (1731-1810) in the famous
Cavendish experiment, as detailed in the figure.
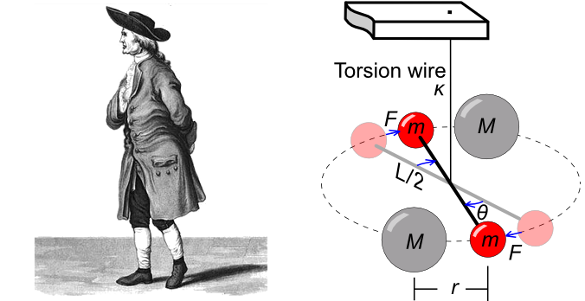
Henry Cavendish (1731-1810), and a diagram of the torsion balance used in the 1798 Cavendish experiment. The larger masses (M) are stationary lead spheres, and the smaller spheres (m) are also made of lead. Gravitational force causes the masses to twist the wire with torsion coefficient κ, which allows a force measurement. The force is so small that the lead spheres were chosen to be huge. The larger spheres were each 350 pounds, while the smaller spheres were each 1.61 pounds. (Left image, an illustration by George Wilson, from "The Life of the Hon. Henry Cavendish," 1851, via Wikimedia Commons. Right image, a diagram by Chris Burks, via Wikimedia Commons.)
As I wrote in an
earlier article (Measuring the Gravitational Constant, November 14, 2014), Cavendish led an interesting scientific life, having also discovered
hydrogen, but a strange personal life. In today's
terminology, Cavendish was a
geek. He wore
clothing that was
out-of-fashion for his time, and he was exceptionally
shy around
women. According to
The Cavendish page on Wikipedia, he had a back door added to his
house so that he could leave without seeing the
housekeeper.
With such knowledge it's possible to apply a
conservation law to the
orbit of the Earth to calculate the mass of the
Sun. The gravitational force holding the Earth and Sun together must equal the
centripetal force that keeps the Earth in its orbit around the Sun. For a
circular orbit of
radius r, the centripetal force is
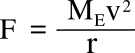
where
ME is the mass of the Earth, and
v is the orbital velocity, easily calculated from the orbital radius and the length of the
year. Once we have the mass of the Sun, it's possible to calculate the mass of the
planets through similar calculations. Planetary orbits are
elliptical, rather than circular, so the centripetal force would vary, but so would the orbital radius
r and the gravitational force. A circular orbit is just a special case of an elliptical orbit that makes such calculations easy.
As the following figure shows, our
Solar System has a vast extent that goes beyond the orbit of the last planet,
Neptune, (after
Pluto's demotion from planet to
dwarf planet) to include the
Kuiper Belt, a
circumstellar disk of small objects similar to the
asteroid belt between
Mars and
Jupiter; and the
Oort Cloud, an
hypothesized cloud of
planetesimals that serves as a reservoir for
comets. The Oort Cloud extends to about 100,000
astronomical units (AU, the Earth-Sun distance), and it marks the physical boundary of the Solar System at about 2
light years. This is not surprisingly half the distance to the
nearest star.
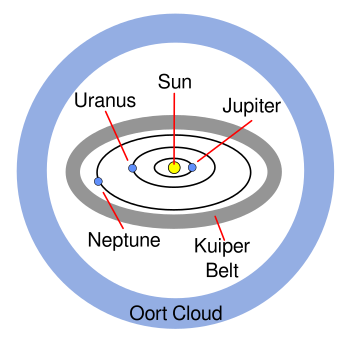
The huge extent of the Solar System (not to scale).
Jupiter is about five times further from the Sun than the Earth, while Neptune is about thirty. Beyond Neptune is the Kuiper Belt at about 30-50 astronomical units (AU, the Earth-Sun distance). Beyond the Kuiper Belt is the Oort Cloud that extends to the limits of the Solar System, about two light years.
(Created using Inkscape. Click for larger image.)
It's easy to sum the masses of the Sun and its planets, but it's harder to calculate the total mass of the Solar System, since the masses of the Kuiper Belt and Oort Cloud can only be
estimated. The vast majority of Solar System mass is in the Sun, since the total mass of Kuiper Belt objects is estimated to be less that a tenth that of the Earth, and the Oort Cloud's mass is about five times Earth's mass.
The next step up on the
cosmological scale is the
Milky Way Galaxy, which may contain up to 400 billion
stars. One way to estimate the mass of the Milky Way would be to assume that our Sun is an average star, and just multiply the mass of the Sun (333,000 Earth masses, or 1.9885 x 10
30 kilograms) by 400 billion to obtain 2 x 10
41 kilograms. That estimate would be wrong, since we've ignored its contained
dark matter, and the
supermassive black hole at its center. This estimate is a factor of ten too small.

Milky Way over Lassen Peak.
Lassen Peak is an active volcano in the Cascade Range in Northern California. Its activity was underscored by an eruption on May 22, 1915, that spread volcanic ash over a large area.
Lassen Volcanic National Park was created to preserve the area and its volcanic features.
(Photo by Alison Taggart-Barone, via Wikimedia Commons.)
In the past, a variety of
observational techniques have been used to estimate the mass of the Milky Way, and these have produced a range of masses from 500 billion solar masses, a trifle above our
back-of-the-envelope calculation above, to 3 trillion solar masses. However, the same technique for finding the mass of the Sun from the mass and motion of the Earth can be applied also to the Milky Way. A team of
astronomers from the
Space Telescope Science Institute (Baltimore, Maryland),
Johns Hopkins University (Baltimore, Maryland), and the
University of Cambridge, (Cambridge, United Kingdom) has produced a new estimate based on the motions of
globular clusters of stars that orbit the Milky Way with data from
NASA's Hubble Space Telescope and the
European Space Agency's Gaia satellite.[1-5]
Hubble and Gaia were used to measure the movements in
three dimensions of globular star clusters, isolated patches of hundreds of thousands of stars that orbit the Milky Way.[2-3] About fifty of these star clusters were formed before creation of the Milky Way's spiral disk, and they can be used to measure the Milky Way's mass.[2-4] Says
Tony Sohn of the Space Telescope Science Institute, who led the Hubble measurements, "Because of their great distances, globular star clusters are some of the best tracers astronomers have to measure the mass of the vast envelope of dark matter surrounding our galaxy far beyond the spiral disk of stars."[2-3] The Hubble-Gaia study was based on a decade of observations of 34 globular clusters out to 65,000 light-years and one cluster out to 130,000 light-years.[2-3]
The
analysis of the motions of the globular clusters gave a Milky Way mass of 1.28 (+0.97-0.48) x 10
12 (about a trillion) solar masses,[1] a mass that makes our galaxy somewhat of a heavyweight, since the lightest galaxies are about a billion solar masses. It's still lighter than some, since the heaviest galaxies are about 30 trillion solar masses.[2-3] In any case, it's assumed that most of its mass is in the form of dark matter.

A computer simulation of the Milky Way Galaxy.
(Portion of a Creative Commons Attribution licensed YouTube Video by Hubble and the European Southern Observatory.)[4]
(Click for animated image of its rotation.)
![]()
References:
- Laura L. Watkins, Roeland P. van der Marel, Sangmo Tony Sohn, and N. Wyn Evans, "Evidence for an Intermediate-mass Milky Way from Gaia DR2 Halo Globular Cluster Motions," The Astrophysical Journal, vol. 873, no. 2 (March 12, 2019), DOI: https://doi.org/10.3847/1538-4357/ab089f; also at arXiv.
- What Does the Milky Way Weigh? Hubble and Gaia Investigate, NASA Press Release, March 7, 2019.
- What Does the Milky Way Weigh? Hubble and Gaia Investigate, Hubblesite Press Release no. 2019-16, March 7, 2019.
- Hubblecast 117 Light: Hubble & Gaia weigh the Milky Way, YouTube Video by Hubble and the European Southern Observatory, March 7, 2019; also at spacetelescope.org.
Linked Keywords: Scientist; experiment; academic conference; scientific conference; chemical thermodynamics; calorimetry; reaction calorimeter; combustion calorimetry; volatile organic compound; liquid; plastic; packet (container); pouch; accuracy and precision; accurate; weight; combustion; combusted; material; experimenter; buoyancy; gas; volume; vapor; density; atmosphere of Earth; air; the best is the enemy of the good; aphorism; diminishing returns; high school; chemistry; significant figures; calculation; calculate; reagent; reactant; product (chemistry); laboratory instrumentation; numerical digit; workbench; benchtop; multimeter; digital; weighing scale; analytical balance; pan balance; career; history; balance scale; commerce; mass; human; classical antiquity; human culture; constellation; Libra (constellation); Latin; word; modern history; star chart; Milky Way; International Astronomical Union; Sidney Hall (1788–1831); United States Library of Congress; Wikimedia Commons; KStars; concept; conceptual; Earth; physics; Newton's law of universal gravitation; Isaac Newton (1642-1727); Philosophae Naturalis Principia Mathematica; gravitation; gravitational; force; CODATA; meter; kilogram; second; Great Britain; British; Henry Cavendish (1731-1810); Cavendish experiment; torsion balance; lead; sphere; wire; torsion coefficient; pound; hydrogen; terminology; geek; clothing; fashion; out-of-fashion; shyness; shy; woman; women; house; domestic worker; housekeeper; conservation law; orbit; Sun; centripetal force; circle; circular; radius; year; planet; ellipse; elliptical; Solar System; Neptune; Pluto; Pluto classification; dwarf planet; Kuiper Belt; circumstellar disk; asteroid belt; Mars; Jupiter; Oort Cloud; hypothesis; hypothesize; planetesimal; comet; astronomical unit; light year; Proxima Centauri; nearest star; Inkscape; approximation; estimate; cosmology; cosmological; star; kilogram; dark matter; supermassive black hole; Lassen Peak; active volcano; Cascade Range; Northern California; volcanic eruption; volcanic ash; Lassen Volcanic National Park; observational astronomy; back-of-the-envelope calculation; astronomer; Space Telescope Science Institute (Baltimore, Maryland); Johns Hopkins University (Baltimore, Maryland); University of Cambridge, (Cambridge, United Kingdom); globular cluster; NASA; Hubble Space Telescope; European Space Agency; Gaia satellite; three-dimensional space; three dimensions; Tony Sohn; analysis; computer simulation; Creative Commons Attribution license; YouTube Video; Hubble Space Telescope; European Southern Observatory.