| Tikalon Blog is now in archive mode.
An easily printed and saved version of this article, and a link
to a directory of all articles, can be found below: |
|
This article |
| Directory of all articles |
Estimation
December 21, 2011
Estimation is an important part of
science. Before starting an
experiment, it's always important to ascertain whether your experiment will actually demonstrate the
hypothesis that you're testing, or
falsify it to a certain
precision. Is there so much variation in
room temperature that a
controlled temperature chamber is needed? Is there too much
noise to see the
signal you're expecting? Are the
statistics such that your supposedly quick and simple experiment would need to run for several months to get a valid result?
Scientists often use a form of estimation called a
back-of-the-envelope calculation. Back-of-the-envelope calculations infer the desired quantity by a very long chain of estimated values through use of simple
models. The most notorious of such calculations is the
Drake equation that estimates the number of detectable
extraterrestrial civilizations in our
Milky Way galaxy.
In its original form, the Drake equation has seven estimated quantities that are multiplied together to give a number of about ten. The
uncertainty in these seven terms is such that the equation might also give a number less than one. If the quantities used in this estimate were better known, and the result was a number in the thousands, or millions, the
SETI community would be encouraged. There is, however, no real solace in the Drake equation.
Nobel physics laureate,
Enrico Fermi, was well known for his back-of-the-envelope calculations; so much so that a particular subset of these is called "
Fermi problems." Fermi problems are estimates of unusual quantities based on whatever information is at hand.
One common example of a Fermi problem is a calculation of the number of
piano tuners in
Chicago. This problem was more interesting when many
households actually had
mechanical pianos, and not
MIDI players on their
computers. This estimate involves quantities such as the fraction of households that have pianos, how often they are tuned, and how long it takes to tune a piano.[1]
Enrico Fermi at a blackboard. The expression for the fine structure constant, α, is wrong. The elementary charge, e should be in the numerator, and the reduced Plank constant, h-bar, should be in the denominator. Fermi's wry smile might indicate an intentional joke.
(Image from the Smithsonian Institution, via Wikimedia Commons))
One famous example of Fermi's estimation ability was his estimate of the
yield from the
Trinity nuclear test based on how far pieces of paper were blown by the
pressure wave of the blast. His back-of-the-envelope calculation, which in this case may have actually involved a shredded envelope as the paper source, gave a value about half the actual value. I would often do similar estimates, such as how many people there might be in our
county, based on the number of
supermarkets, much to the derision of my wife and children.
Even after careful estimation of the operating conditions for my experiments, time would still seem to stand still while I was waiting for my
analysis programs to crank through the results to determine whether all went well. My estimation of time, however, was wildly incorrect. A recent study shows a connection between a person's accuracy in the estimation of time intervals and
mathematical ability.[2]
Psychologists at the
Dipartimento di Psicologia Generale, the
University of Padova (Padova, Italy), did a combined study of participants' mathematical ability and their ability to estimate the duration of a tone.[2]
The study participants were presented with 250
Hz tones of varied duration. The tones had 10
millisecond leading and falling ramps to preclude any perceived "click." The tones, presented at 100, 200, 500, 1000, and 3000 millisecond durations, were repeated six times, and they were repeated in
random order.
Arithmetic ability was measured using the arithmetic subset of the the WAIS-R version of the
Wechsler Adult Intelligence Scale. This arithmetic subtest was used as a measure of mathematical
intelligence.[2]
As can be seen in the figure, when the study participants were divided into low and high math achievers, there was a definite
correlation between time estimation and mathematical capabilities. The study authors conclude that this correlation is likely the result of a common reliance on
spatial ability for these two tasks.[2]
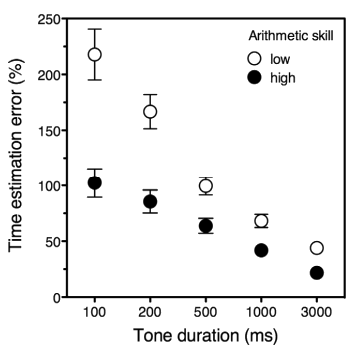
Error in tone interval estimation as a function of tone duration for low and high math achievers.
The split in ability is clearly seen.
(Fig. 1 of ref. 2).[2])
![]()
References:
- One of my managers, an optical physicist, was also a trained piano tuner. He played a wind instrument, not the piano.
- P. Kramer, P. Bressan and M. Grassi, "Time Estimation Predicts Mathematical Intelligence," PLoS ONE, vol. 6, no. 12 (December, 2011), Document No. e28621.
Permanent Link to this article
Linked Keywords: Estimation; science; experiment; hypothesis; falsifiability; precision; room temperature; controlled temperature chamber; noise; signal; statistics; back-of-the-envelope calculation; scientific model; Drake equation; extraterrestrial civilizations; Milky Way galaxy; uncertainty; search for extraterrestrial intelligence; SETI; Nobel Prize in Physics; Nobel laureate; Enrico Fermi; Fermi problems; piano tuners; Chicago; household; mechanical piano; MIDI player; computer; fine structure constant; elementary charge; Plank constant; Smithsonian Institution; Wikimedia Commons; nuclear weapon yield; Trinity nuclear test; pressure wave; county; supermarket; data analysis program; mathematics; psychologist; Dipartimento di Psicologia Generale; University of Padova (Padova, Italy); Hertz; Hz; millisecond; random; arithmetic; Wechsler Adult Intelligence Scale; intelligence; correlation; spatial visualization ability.