Arrhenius Law
September 13, 2021
While the
human body has difficulty performing tasks such as
lawn mowing and
gardening in the
summer's heat, heat enhances the performance of machinery operating as
heat engines. According to the
second law of thermodynamics, a
temperature difference is required to perform
work, and the
equation for the maximum
efficiency of a heat engine, the
Carnot efficiency η, reveals that the larger the temperature difference, the better.
ηCarnot = (Thot-Tcold)/Thot

One of the more famous high school yearbook portraits - Sadi Carnot (1796-1832) in 1813 at age 17 in his uniform for the École Polytechnique.
Carnot, who is called the father of thermodynamics, served as a mechanical engineer in the French Army. He ppublished a book in 1824, "Reflections on the Motive Power of Fire," that contained his theory of the maximum efficiency of heat engines that became the basis for the second law of thermodynamics and its concept of entropy.
One fundamental concept of his book was that heat engines are more efficient when the temperature of their heat reservoir is increased.
(An engraving by Louis-Léopold Boilly (1761–1845) via Wikimedia Commons. Click for larger image.)
Gas turbines, such as those for
jet engines, are heat engines for which temperatures are pushed to extremes to gain efficiency. The
thermodynamic cycle for these is the
Brayton cycle. In such turbine engines,
air is compressed, mixed with
fuel, and
combusted. The resultant high temperature
flow is used to drive the
compressor, and
rotary devices, such as
electrical generators, to create useful work. In an
aircraft, the
hot exhaust will produce
thrust. The following figure illustrates the maximum efficiency of a Brayton cycle engine as a
function of the temperature between the inlet (at 298 K) and the outlet.
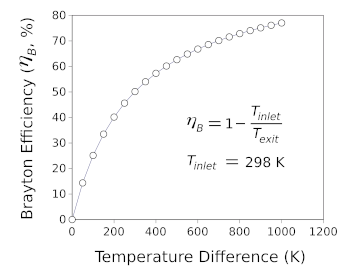
The maximum efficiency, ηB, of a Brayton cycle engine as a function of the difference in temperature between the exit and inlet when the inlet temperature is 298 K.
Materials scientists work to create turbine blade materials and coatings that allow operation at higher temperatures. At a difference temperature of 1000 K (an operating temperature of about 1025 °C) the slope is 0.02%/K.
(Created with Gnumeric. Click for larger image.)
I've done many
calculations in which
precise data are unavailable, and for these I've used various
rules of thumb, such as
Trouton's rule that the
entropy of vaporization is almost always 85
J/
K-
mol) for a
liquid at its
boiling point. One common rule of thumb in
chemistry is that
reaction rates double for every temperature increase of ten degrees
Celsius (or
kelvin). This rule derives from an important equation, the
Arrhenius equation, derived from
statistical mechanics by
physical chemist,
Svante Arrhenius (1859-1927), who was awarded the 1903
Nobel Prize in Chemistry.
The Arrhenius equation allows calculation of the
rate constant of a
chemical reaction based on an
activation energy and the
absolute temperature. It appears here in two equivalent forms, depending on the
units used:
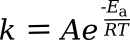
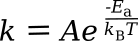
in which k is the rate constant, T is the absolute temperature (K), A is a constant for each particular reaction, E
a is the activation energy for the reaction, R is the
gas constant, and k
B is the Boltzmann constant. Taking
ratios at
room temperature shows a doubling of rate if the activation energy is 52.9 kJ/mol. Not all reactions will have this value, but it's likely a good
average.
The equation was conceived in 1889 by Arrhenius, who reasoned that
reactants need to have sufficient
kinetic energy in order to merge with each other to form a
product. Through statistical mechanics, a given temperature will produce a fraction of
molecules with kinetic energy greater than the activation energy, and that fraction is the rate constant in a
reversible reaction.

Physical chemist, Svante Arrhenius (1859-1927), who was awarded the 1903 Nobel Prize in Chemistry.
Arrhenius was the first to realize that atmospheric carbon dioxide would increase Earth's surface temperature.
The lunar crater, Arrhenius, and the Martian crater, Arrhenius, are named in his honor.
(Portion of a Wikimedia Commons image from Zeitschrift für Physikalische Chemie (1909). Click for larger image.)
In
pre-computer times,
chemists would deduce the activation energy from a
plot of the
logarithm of the rate constant against
inverse temperature, 1/T. In this plot, called an
Arrhenius plot, the slope is (E
a/R) and the y-intercept at 1/T = 0 is the log of the
scale factor, A.
Computer applications now give these values by a
linear regression of the data.
To demonstrate the
ubiquity of the
Arrhenius law,
Keith J. Laidler (1916-2003) of the
University of Ottawa (Ottawa, Canada) published a paper in the
Journal of Chemical Education in 1972 in which he included data showing that the
chirping frequency of
tree crickets (Oecanthus) follows the
Arrhenius Law. The data, plotted in the figure, gives an activation energy of 12.2
kcal/mol (51 kJ/mol).
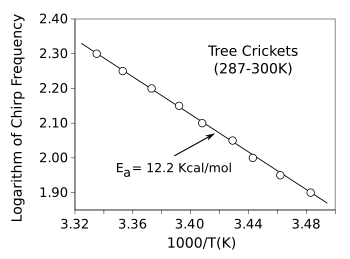
Arrhenius law for the chirping frequency of tree crickets (Oecanthus).
The frequency of flashing of fireflies gives the same activation energy, 12.2 kcal/mol, but with more scatter of data points.[1]
(Created using Gnumeric from data if ref. 1. Click for larger image.)
Axel Lorke, a
professor of
physics at the
University of Duisburg-Essen, has recently published an article about the Arrhenius law in
Physics Today.[2] In that article he shows that
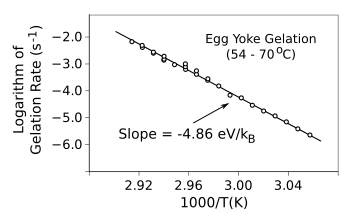
egg yoke gelation, the point at which the
viscous and elastic moduli are equal, obeys the Arrhenius law. He was fortunate in obtaining gelation data from a
decade old paper by
researchers who were willing to wait a hundred
hours for some data (see graph).[3]
"I'll have my eggs sous vide - cook for a hundred hours at 54 °C."
Egg yoke gelation follows the Arrhenius law.
(Created using Gnumeric from data in refs. 2-3. Click for larger image.)
References:
- Keith J. Laidler, "Unconventional Applications of the Arrhenius Law," Journal of Chemical Education, Vol. 49, No. 5 (May 1972), pp. 343f..
- Axel Lorke, "Boiling eggs, radiation damage, and the Arrhenius plot," Physics Today, vol. 74, no. 5 (May 1, 2021), pp. 66f., https://doi.org/10.1063/PT.3.4757.
- César Vega and Ruben Mercadé-Prieto, "Culinary Biophysics: on the Nature of the 6X°C Egg, Food Biophysics, vol.6, no. 1 (March, 2011) 152-159 (2011). https://doi.org/10.1007/s11483-010-9200-1.
Linked Keywords: Human body; lawn mowing; gardening; summer; heat; heat engine; second law of thermodynamics; temperature; work (physics); equation; energy conversion efficiency; Carnot's theorem (thermodynamics); Carnot efficiency; Sadi Carnot in 1813 at age 17; fame; famous; secondary school; high school; yearbook; portrait; Sadi Carnot (1796-1832); uniform; École Polytechnique; thermodynamics; mechanical engineering; mechanical engineer; French Army; academic publishing; published; book; Reflections on the Motive Power of Fire; theory; entropy; Louis-Léopold Boilly (1761–1845); Wikimedia Commons; gas turbine; jet engine; thermodynamic cycle; Brayton cycle; compressed air; aviation fuel; combustion; combust; airflow; compressor; rotation; rotary; electric generator; electrical generator; aircraft; exhaust gas; thrust; function (mathematics); Brayton cycle efficiency as a function of temperature differential; Brayton cycle; materials science; materials scientist; turbine blade; material; coating; slope; Gnumeric; calculation; accuracy and precision; precise; data; rules of thumb; Trouton's rule; entropy of vaporization; joule; kelvin; mole (unit); mol; liquid; boiling point; chemistry; reaction rates; Celsius; Arrhenius equation; statistical mechanics; physical chemistry; physical chemist; Svante Arrhenius (1859-1927; Nobel Prize in Chemistry; reaction rate constant; chemical reaction; activation energy; thermodynamic temperature; absolute temperature; units of measurement; gas constant; ratio; room temperature; mean; average; reagent; reactant; kinetic energy; product (chemistry); molecule; reversible reaction; carbon dioxide in Earth's atmosphere; atmospheric carbon dioxide; Earth; global surface temperature; Moon; lunar; impact crater; Arrhenius (lunar crater); Mars; Martian; Arrhenius (Martian crater); pre-computer; chemist; plot (graphics); logarithm; multiplicative inverse; Arrhenius plot; scale factor; application software; computer application; linear regression; ubiquity; Arrhenius law; Keith J. Laidler (1916-2003); University of Ottawa (Ottawa, Canada); Journal of Chemical Education; stridulation; chirping; frequency; tree cricket (Oecanthus); kilocalorie per mole; kcal/mol; firefly light and chemical production; flashing; fireflies; Gnumeric; Axel Lorke; professor; physics; University of Duisburg-Essen; Physics Today; egg yoke; gelation; iscoelasticity; viscous and elastic moduli; decade; research; researcher; hour; egg (food); sous vide; cooking; cook.