Cubic Earth
September 7, 2020
It's easy to find the important things in life, since they're usually
taxed.
Salt has been taxed through most of
history.
Salt is
essential to life, since it supplies
sodium ions that are the means for
nerve impulse generation, proper functioning of the
heart, and
fluid balance.
Salting is used as an easy means of
food preservation, since the
dehydrating action of salt
kills most
bacteria,
fungi and other
pathogens. Salt is also a much used
food seasonings. I use a pinch of salt in my
morning coffee, since it reduces the
bitter taste,[1] but this is not recommended for people with
hypertension.
A tax on salt in
China around 300
BC was the main source of funding for the
Great Wall. A salt tax was imposed in
France in 1360, and in
England in 1693, where it was doubled in just three years,
repealed in 1825 and then established under
British-ruled India from 1835. The word
salary comes from the
Latin word for salt,
sal, a
salarium ("salt money") being paid to
Roman soldiers for the
purchase of salt.

Left image, crystals of Halite (rock salt) created by slow crystallization from a concentrated salt solution at room temperature. Right image, the crystal structure of sodium chloride (NaCl) with the larger chlorine anions shown in green. While we think of salt in the context of food, most of the 250 million tons of annual production are used in chemical processes. (Left image; and, right image by Benjah-bmm27, both from Wikimedia Commons)
The
mineral crystal form of salt (
sodium chloride, NaCl) is called
Halite. This crystal, also known as rock salt, takes the shape of its underlying
crystal structure (see figure). This is true for many minerals. The crystals are
cubic, and the crystal structure is
cubic; specifically, the
halite structure that's found in many other
compounds. If you ignore the fact that the crystal is built from two different types of
atoms, it's the simplest cubic structure known appropriately as "
simple cubic." It can be viewed as interpenetrating
face-centered cubic lattices of
sodium and
chlorine atoms.
A cube is one of the five
Platonic solids. Platonic solids are the regular,
convex polyhedrons, the
tetrahedron,
cube,
octahedron,
dodecahedron, and
icosahedron, as shown in the table.
Plato (c.428 BC-c.348 BC), in his c. 360 BC
Timaeus, associated each of the
four classical elements (
earth,
air,
water, and
fire) with one of the regular polyhedra.[2] Earth was associated with the cube, air with the octahedron, fire with the tetrahedron, and water with the icosahedron.
Aristotle, perhaps seeing that one of these, the dodecahedron, was not associated, added a fifth element, the
Aether. Interestingly, on a
macroscopic scale, there aren't too many cubes or
squares in
nature. You're more likely to see
hexagons, a preferred shape, since hexagons can
tile two-dimensional space.
While cubes seem to appear only rarely found in nature, a recent
article in the
Proceedings of the National Academy of Sciences demonstrates that cubes will arise when fragments of natural
materials are appropriately
averaged. This is a consequence of the
isotropic stress conditions that formed them.[3-5] In simple language, it was found that when
rocks break apart, the result is a bunch of cubes.[5] This rule seems to apply generally to materials over a size range from
microscopic to
planetary.[5] The
research team had members from the
University of Pennsylvania (Philadelphia, Pennsylvania), the
Budapest University of Technology and Economics (Budapest, Hungary), and the
University of Debrecen (Debrecen, Hungary).[4]
Says
Douglas Jerolmack, a
geophysicist at the University of Pennsylvania and one of the study
authors,
"It turns out that Plato’s conception about the element earth being made up of cubes is, literally, the statistical average model for real earth. And that is just mind-blowing... If you take a three-dimensional polyhedral shape, slice it randomly into two fragments and then slice these fragments again and again, you get a vast number of different polyhedral shapes. But in an average sense, the resulting shape of the fragments is a cube."[4]
This research was inspired by
geometrical models developed by
Gábor Domokos, a
mathematician at the Budapest University of Technology and Economics. In 2006, Domokos and
colleagues showed the existence of the
gömböc, a
gemstone-like shape that has only one stable balance point
conjectured in 1995 to exist. Domokos and his colleagues found that natural materials
erode toward this shape but never quite reach it.[5] The early geometrical models also predicted the fragmentation of natural rocks into cubes.[4]

Cubism or Gömböcism? The left image is a 1912 oil on canvas portrait of Portrait of Pablo Picasso by Juan Gris (1887-1927) done in the Cubist style and presently at the Art Institute of Chicago. On the left is the structure of a Gömböc, a shape described in the text. (Left image, a Wikimedia Commons image from the Google Art Project. Right image, a modified Wikimedia Commons image by vierkantswortel2.)
One possible reason why materials fragment into cuboid shapes is that the fragments must still fit together without any gaps, and the cube is a regular polyhedron with sides of equal length that does that.[3-4] As Jerolmack explains, "It turns out in
two dimensions you're about equally likely to get either a
rectangle or a hexagon in nature... They're not true hexagons, but they’re the statistical equivalent in a geometric sense. You can think of it like
paint cracking; a
force is acting to pull the paint apart equally from different sides, creating a hexagonal shape when it
cracks."[4]
The research team used a
supercomputer to
model the fracture of three-dimensional materials under an idealized condition in which it's pulled equally in all directions. This produced polyhedrons that are
ostensibly cuboid.[5] The team then searched for real world examples of this tendency, both in existing
datasets and fragmentation patterns of rocks they collected.[4] One example, a
dolomite mineral deposit near
Budapest, Hungary, had objects with the expected cuboid fragments, regardless of whether they had been created naturally, or through
dynamiting the deposit.[4-5]
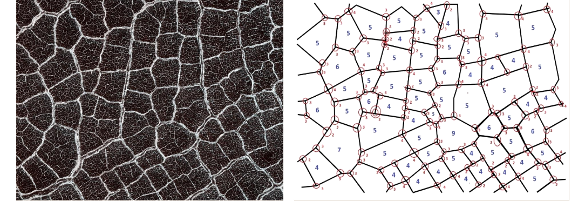
An image of a patterned surface on Mars on the left is analyzed to extract its polygonal shapes (right). The average vertex number is found to be about 4.9, closer to a pentagon than a square. This is a portion of Fig. S6, supplementary information from ref. 3. The image of Mars is a NASA/JPL-Caltech/University of Arizona image.
This fracture into cubes doesn't happen just here, on Earth, but elsewhere in the
Solar System.[4] However, at base, this
phenomenon is just an
approximation. As Jerolmack explains, "The world is a messy place... Nine times out of 10, if a rock gets pulled apart or squeezed or sheared - and usually these forces are happening together - you end up with fragments which are, on average, cubic shapes."[4] Minerals will
cleave according to their crystal structure; for example,
mica breaks into
sheets, and they do not follow the results of the simulations since they do not have isotropic mechanical properties.[5] Says Jerolmack,
“When you pick up a rock in nature, it’s not a perfect cube, but each one is a kind of statistical shadow of a cube... It calls to mind Plato’s allegory of the cave. He posited an idealized form that was essential for understanding the universe, but all we see are distorted shadows of that perfect form."[4]
The
data for this research is available at the
Center for Open Science (
https://osf.io/h2ezc/), and the
computer code can be found at
GitHub (
https://github.com/torokj/Geometric_fragmentation).

Humans have always looked for regularity in nature. On the right is Johannes Kepler's (1571-1630) Platonic solid model of the Solar System from his 1596 Mysterium Cosmographicum. The cubic Earth image was created using Inkscape. The "Blue Marble" Earth image, taken by the crew of Apollo 17, December 7, 1972, is from Wikimedia Commons. On the right is a modified Wikimedia Commons image.
References:
- P. A. S. Breslin and G. K. Beauchamp, "Salt enhances flavour by suppressing bitterness," Nature, vol. 387 (June 5, 1997), pp. 563ff., https://doi.org/10.1038/42388.
- Plato, "Timaeus," Benjamin Jowett, Trans., at the The Internet Classics Archive by Daniel C. Stevenson.
- Gábor Domokos, Douglas J. Jerolmack, Ferenc Kun and János Török, Plato's cube and the natural geometry of fragmentation," Proceedings of the National Academy of Sciences, July 17, 2020, DOI: 10.1073/pnas.2001037117.
- Plato was right. Earth is made, on average, of cubes, University of Pennsylvania Press Release, July 20, 2020.
- Adam Mann, "From rocks to icebergs, the natural world tends to break into cubes," Science, July 27, 2020, doi:10.1126/science.abe0397.
Linked Keywords: Tax; taxed; salt; salt tax; history; essential nutrients; sodium in biology; sodium ion; nerve; action potential; impulse generation; heart; fluid balance; salting (food); food preservation; hygroscopy; dehydrating action; disinfectant; kill; bacteria; fungus; fungi; pathogen; food; seasonings; morning; coffee; taste; bitterness; bitter taste; hypertension; China; Anno Domini; BC; Great Wall of China; France; England; repeal; repealed; British Raj; British-ruled India; salary; Latin; sal; salarium; Ancient Rome; soldier; purchase; crystal; Halite (rock salt); crystallization; concentration; concentrated; brine; salt solution; room temperature; crystal structure; sodium chloride (NaCl); chlorine; anion; ton; annual; production (economics); chemical reaction; chemical process; Benjah-bmm27; Wikimedia Commons; mineral; crystal; cube; cubic; cubic crystal system; halite crystal structure; chemical compound; atom; simple cubic crystal; face-centered cubic crystal; lattice; sodium; Platonic solid; convex polytope; convex polyhedron; tetrahedron; cube; octahedron; dodecahedron; icosahedron; Plato (c.428 BC-c.348 BC); Timaeus; four classical elements; earth (classical element); air (classical element); water (classical element); fire (classical element); Aristotle; Aether (classical element); macroscopic scale; square; nature; hexagon; tile; two-dimensional space; scientific literature; article; Proceedings of the National Academy of Sciences; material; average; isotropy; isotropic; stress (mechanics); rock (geology); microscopic; planet; planetary; research; University of Pennsylvania (Philadelphia, Pennsylvania); Budapest University of Technology and Economics (Budapest, Hungary); University of Debrecen (Debrecen, Hungary); Douglas Jerolmack; geophysics; geophysicist; author; conjecture; conception; statistics; statistical; randomness; random; geometry; geometrical; conceptual model; model; Gábor Domokos; mathematician; colleagues; gömböc; gemstone-like; conjecture; conjectured; erosion; erode; Cubism; Gömböcism; oil on canvas; portrait; Pablo Picasso; Juan Gris (1887-1927); Cubist; Art Institute of Chicago; Google Art Project; two-dimensional space; rectangle; paint; fracture; cracking; force; supercomputer; mathematical model; ostensibly; dataset; dolomite; mineral deposit; Budapest, Hungary; dynamite; dynamiting; pattern; patterned; surface; Mars; analysis; analyzed; polygon; polygonal; average; vertex (geometry); vertex number; pentagon; square (geometry); Solar System; phenomenon; >approximation; cleavage (crystal); cleave; mica; lamella (materials); sheet; Plato’s allegory of the cave; theory of forms; idealized form; universe; shadows; data; Center for Open Science; computer code; GitHub; human; nature; Johannes Kepler (1571-1630); Platonic solid; Mysterium Cosmographicum; Inkscape; "Blue Marble" Earth image; Apollo 17.