Algorithmic Music
January 19, 2011
Musical composition is a lot like
theorem generation in
mathematics. You have a set of rules, and you turn the crank to generate something interesting within that rule set. It sounds mechanical and not at all creative; but it's the "something interesting" part that differentiates good composers and good mathematicians from mere hacks. The idea that you can
generate music algorithmically has been with us longer than computers. A method of generating music by stringing together short musical phrases randomly, usually by casting lots, was popular in the eighteenth century. This technique was known as
Musikalisches Würfelspiel, or the Musical Dice Game.
Joseph Haydn composed such an algorithmic composition, called the Philharmonic Joke, in 1790; but the most famous example of this type of composition is ascribed to
Mozart. Mozart's method was sold as a game by his publisher in 1792, although we're not sure that Mozart approved. In this game, musical phrases were randomly selected by dice throws to piece together musical compositions. You can try Mozart's game using an
online implementation,[1] or you can hear a
minuet that was generated for me,
now.
I was interested in
electronic music from an early age, and I designed and built several
electronic music synthesizers in the 1970s. Recently, I was surprised to find that one of my experimental circuits has seen a
revival on the Internet. I dabbled with
algorithmic computer composition in my graduate schools days when I had access to a
nice mainframe, but a turning point was the publication of the article, "1/f-noise in music and speech," by Richard F. Voss and John Clarke in a 1975 issue of
Nature.[2] Voss subsequently communicated to
Martin Gardner a simple algorithm for generating 1/f-noise via dice throws. This was essentially a
low pass filter applied to the casting of multiple dice. A simple C language implementation that generated the data shown in the figure can be found
here.
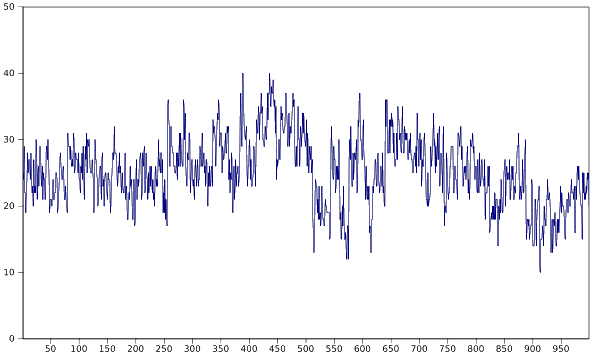
A thousand samples of 1/F noise calculated by the Voss dice-throwing algorithm. See Ref. 3.[3]
Not only was the Voss algorithm, which I generalized to dice with
n faces, useful for generating music, but I wrote a program that used it to simulate my typing on a
daisy-wheel printer. When my office door was closed, the cadence sounded so human that everyone believed I was actually hard at work on a manuscript while I was really elsewhere, playing in my lab. With the demise of impact printers and the transition from actual
typing to
electronic word processing, you'll need to find some other technique. I hear that the fake
teleconference works just as well.
I was reminded of all this when I read a review of an exhibit at the
Los Angeles Museum of Contemporary Art, Pacific Design Center, about the work of composer,
Iannis Xenakis (May 29, 1922 - February 4, 2001).[4] Xenakis is known for his use of algorithmic composition techniques, but few know that he worked originally as an
architect and was employed by
Le Corbusier in
Paris. He left Le Corbusier in 1959 in a dispute about Le Corbusier's taking too much credit for Xenakis' designs, including the very geometrical
Philips Pavilion of the Brussel's
Expo-58. This pavilion was composed of
hyperbolic paraboloids, a shape that Xenakis realized would diffuse echoes.

Iannis Xenakis
(Courtesy of Friends of Xenakis).
While working as an architect, Xenakis studied musical composition, but he had a difficult time finding a teacher who ascribed to his different ideas about music. Xenakis wanted to transform geometrical drawings into music, something quite out of the mainstream in the fifties. He went through a veritable laundry list of Parisian music teachers, including
Nadia Boulanger,
Arthur Honegger and
Darius Milhaud, before settling with
Olivier Messiaen. It's not surprising that Messiaen also tutored
Karlheinz Stockhausen. Messiaen told Xenakis to forget the usual curriculum of
harmony and
counterpoint and concentrate on application of his
geometry and
mathematics training to music. His training with Messiaen emphasized
rhythm.
Xenakis was drawn to computing from its earliest days. His main contribution to computer music was
UPIC, a tablet-based system in which the composer can draw waveforms and sketch the temporal and
timbral parameters of a composition. Xenakis completed his UPIC system in 1977 at the Centre d'Etudes de Mathématique et Automatique Musicales, Paris. UPIC was used in composition by
Jean-Claude Risset and
Curtis Roads. There have been attempts to port the system to personal computers, one of which is HighC.[5]
References:
- John Chuang, "Mozart's Musikalisches Würfelspiel - A Musical Dice Game for Composing a Minuet," 1995.
- Richard F. Voss and John Clarke, "'1/fnoise' in music and speech," Nature, vol. 258, no. 5533 (November 27, 1975), pp. 317-318.
- Martin Gardner, "Fractal Music, Hypercards and more...," W.H. Freeman and Company, New York, 1992, pp. 12-18.
- Jonathon Keats, "How an architect took music back to mathematical roots," New Scientist, December 6, 2010.
- HighC web Site.
- Squidoo - Experimental Computer Music and Electronic Music Creation Web Site.
Permanent Link to this article
Linked Keywords: Musical composition; theorem; mathematics; algorithmic composition; Musikalisches Würfelspiel; Joseph Haydn; Mozart; minuet; electronic music; electronic music synthesizer; vosim; algorithmic computer composition; IBM System/360; Nature; Martin Gardner; low pass filter; Diablo 630; daisy-wheel printer; typewriter; electronic word processing; teleconference; Los Angeles Museum of Contemporary Art, Pacific Design Center; Iannis Xenakis; architect; Le Corbusier; Paris; Philips Pavilion; Expo-58; hyperbolic paraboloid; Nadia Boulanger; Arthur Honegger; Darius Milhaud; Olivier Messiaen; Karlheinz Stockhausen; harmony; counterpoint; geometry; mathematics; rhythm; UPIC; timbre; Jean-Claude Risset; Curtis Roads.