Tikalon Blog by Dev Gualtieri

Squeeze Bottles

January 30, 2023

Dripping water faucets were a curse upon every household before the development of better elastomers to replace natural rubber for faucet washers and gaskets. There are now washerless faucets designed with closely fitting ceramic disks with triangular cutouts that limit the water flow and don't need washers.

A water drop striking the bottom of a metal kitchen sink.

There are a few techniques to mitigate the annoying sound of the water drops from a dripping water faucet before the washer is replaced.

You can wrap a towel around the faucet and direct the other end into the drain; attach a piece of string, sewing thread, or dental floss, to the faucet so that the drip slides down the fiber into the drain; or, place a tall bottle under the faucet so that the water slides down the outside of the bottle.

For a double basin sink, direct the drips to slide down the basin divider; or, submerse the faucet in a tall tumbler filled with water. The excess water from the drips will slide down the side of the container.

(Wikimedia Commons image by Omegatron)

Water drips can be useful. Water clocks in which water drips from one container to another to mark the passage of time were used by people in antiquity. The ancient Greeks named these clepsydra, but water clocks were found in many other cultures, such as Egypt, Babylon, and Persia, as far back as the 16th century BC. The Roman engineer and architect, Vitruvius (c. 80–70 BC - c. 15 BC), wrote about water clocks in Book IX, Chapter 8, of his De architectura.[1]

As anyone who has used a large funnel has noticed, the flow rate through the orifice is rapid when the liquid level is high, and it slows at the end of its discharge. That's because liquid at the top falls from a higher height, and its gravitational force gives a higher pressure at the exit orifice, a principle known as hydraulic head. This phenomenon was quantified by Italian physicist, Evangelista Torricelli (1608-1647). Torricelli's law gives the speed at which a fluid exits a hole in a container as a function of the height of the fluid above the hole. According to this law, the exit speed v is given as

where g is the gravitational acceleration, about 9.8 m/sec² at Earth's surface, and h is the height of the fluid above the hole. A decade ago I experimented with the design of a digital water clock, the basic principle of which is shown in the figure. An optical interrupter is connected to a microcontroller to mark the passage of time by counting the water droplets as they fall through the gap. The drop rate is the equivalent of the flow rate, and a data analysis to verify Toricelli's Law is straightforward.

For the data shown in the figure, the container held about three cups of water (about 700 mL), the initial fluid level was four inches, and it was reduced to one inch over the course of the experiment. As can be seen, Torricelli's Law is verified over this small change in fluid height as a straight line fit when the drop rate is plotted against the square-root of the fluid height.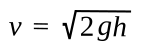

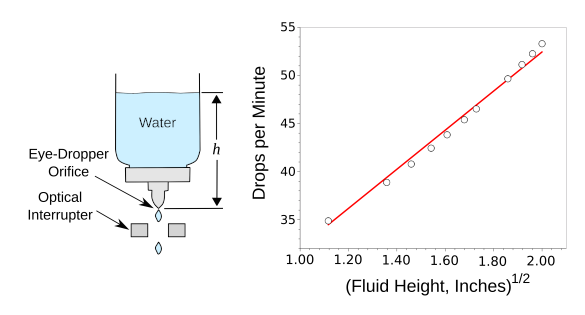
On the left is a schematic diagram of the water drop assembly for the water clocks. The optical interrupter sensed the passage of each water drop. On the left is data collected that verifies Torricelli's law by showing a straight line fit when the drop rate is plotted against the square-root of the fluid height. (Left image created using Inkscape. The data on the right graphed using Gnumeric. Click for larger image.)

My water clock was to have solved the problem of changing drop rate as water is lost by pumping water from a basin back to the upper reservoir. I even designed a circuit to synthesizer a bloop sound to mark the passage of each drop. I used distilled water to prevent anything from clogging the dropper orifice. Unfortunately, the drop rate unexpectedly diminished over time, a phenomenon that I attributed to microscopic air bubbles adhering to the inside of the dropper orifice to restrict the water flow.

room temperature water is a low viscosity Newtonian fluid with mathematically simple fluid flow behavior. Common kitchen condiments, such as ketchup, mustard, and mayonnaise, are non-Newtonian fluids whose viscosity will change when under force to become less viscous and more liquid. Such condiments are sold in convenient squeeze bottles; and, as most of us know, squeezing that last portion from such bottles often leads to an explosive splatter.

Would you prefer ketchup, or catsup, on your French fries?

The popular tomato condiment was generally called catsup in the past, but ketchup is presently the preferred spelling.

These are three of the squeeze bottles in my refrigerator; so, you now know my brand preferences. I should switch to glass bottles, since glass is more likely to be properly recycled than plastic.

(Photo by the author.)

Callum Cuttle and Christopher MacMinn of the Department of Engineering Science at the University of Oxford performed experiments on this effect.[3-5] They presented their research at the American Physical Society's Division of Fluid Dynamics conference (Indianapolis, Indiana) in November of last year,[4] and a preprint of their research is avaibale at arXiv.[3]

When bottles like the ones shown above are squeezed, the air in their inner volume is compressed, this pushes the viscous contents through the exit orifice, but the material's viscosity resists its flow.[4] The Oxford University engineers created an idealized experiment in which air is injected by a syringe pump into a capillary tube filled with silicone oil (see figure).[3-4]

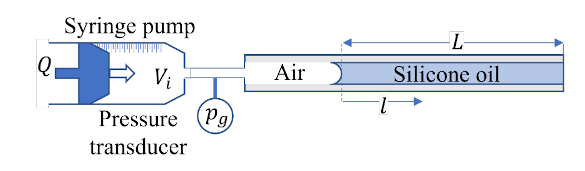
In the experiments, the displacement of silicone oil from a capillary tube is caused by the injection of air from a reservoir of initial volume V_i that's compressed at a constant volume rate Q by a syringe pump. The displacement of the interface as a function of time l(t) relative to its initial position (l(0) = 0) and the gauge pressure p_g of the gas are measured. The initial length of the silicone oil region is L. (Fig. 1(a) of ref. 3.)[3]

Although the experimental system is simple, it does replicate the essential properties of this type of flow.[4] It was found that this process could be modeled by a single dimensionless compressibility number, which depends things such as the amount of air, the diameter of the exit orifice, and the rate of air compression.[3-4] A critical value of this compressibility number defines a transition between two regimes, with the high-compressibility regime showing the burst-like expulsion with which many of us are familiar.[3]

As paper co-author, Callum Cuttle, explains,

"Our analysis reveals that the splattering of a ketchup bottle can come down to the finest of margins: squeezing even slightly too hard will produce a splatter rather than a steady stream of liquid."[4]

To avoid the splatter, you could squeeze the bottle more slowly to reduce the rate of gas compression. Howver, the most effective technique would be a bottle designed with a larger diameter exit orifice, since the larger diamter results in a larger area that reduces the viscous drag.[4] Says Cuttle, the main culprit is the rubber exit valve.

"These valves make the spattering problem worse by forcing you to build up a certain amount of pressure before the sauce can even start to escape. These valves help to avoid leaks, but purely from a splattering perspective, removing these valves would make a lot of sense. For a quick remedy, when you get close to the end of a bottle (when a splatter is most likely), just take the cap off and squeeze the remaining liquid out of the broader neck. It's common sense, but now there is a rigorous mathematical framework to back it up."[4]

Beyond the kitchen, this research can have application in other areas that involve displacement of a fluid with a gas.[4] These include the storage of captured carbon dioxide in aquifers, some types of volcanic eruption, the re-inflation of collapsed lungs, and in fuel cells.[4]

Squeeze Bottles

References: