
Random Walks
June 17, 2023 Stumblebum is a word from my childhood that's not commonly used today. Its meaning as an alcoholic derelict began in 1932, and its frequency of use surged in the late 1940's, around the time of my birth, to 4 parts per billion and is now at 5 parts per billion;[1] so, if you read 200 million words, about the number of words in 2,000 novels, you'll see it just once. I've always associated stumblebum with the so-called drunkard's walk, a type of random walk.
These are the first few steps of a 23,000 step random walk, shown in animation by clicking the figure.
I've created a simple C language program for generating a file of the (x,y) coordinates of such a walk (source code here), and the walk is easily graphed from that file using Gnumeric or Gnuplot.
(Animated 25 000 step random walk (GIF image) by László Németh, via Wikimedia Commons available by Clicking the image.)
In the walk described above, you're allowed to step over any portion of the path created earlier. There's another type of random walk for which this path-crossing is disallowed. This walk, usually done on a two dimensional square lattice, is the self-avoiding random walk. It's as if you're building a brickwall behind you as you walk, and that wall prevents your crossing your prior path. When I decided to implement such a walk on an 8 x 8 lattice, I discovered two things. First, there were no C language examples; and, second, it was conjectured that such a walk on an 8 x 8 lattice was impossible to brute force on a home computer. I was able to find six full-tour walks in a few days on my not very speedy Linux desktop computer[2] using a C language program (Source code here). These six solutions yield many more solutions though reflection and rotation operations. I also wrote an enhanced C language program that collects statistics on the brute-force searches (Source code here).

Six full-tour self-avoiding random walks on an 8x8 two dimensional square lattice as discovered by my C language program. (Graphed using Gnumeric. Click for larger image.)
The first example in the figure above (leftmost, top row) is not that interesting, since it has several long straight sections. This brings us to the idea of tortuosity, a measure of the deviation of a path from a straight line. This is an important parameter for prediction of the transport properties of porous materials, and there are mathematical methods for its calculation for different cases. For our self-avoiding random walk, we can just use the ratio of the number of direction changes to the maximum possible number (62). The calculated tortuosities for the examples in the above figure, clockwise from the upper leftmost, are 0.339, 0.677, 0.677, 0.484, 0.565, and 0.516.
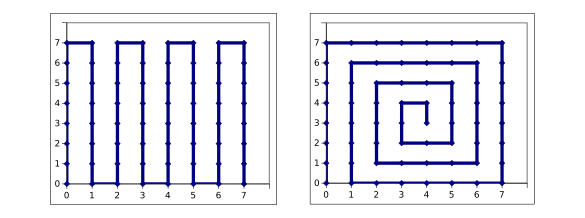
Examples of low tortuosity paths - A zig-zag and spiral walk on an 8x8 two dimensional square lattice. In both cases, the calculated tortuosity, defined as the ratio of the number of direction changes to the maximum possible number of direction changes (62), is 0.226. (Click for larger image.)
Writing about the drunkard's walk reminds me of the observational bias problem known as the streetlight effect, but also called the drunkard's search principle. This is when you only search for something where it is easiest to look. I've been guilty of this myself in a different sense by only doing experiments with the chemicals I have on my laboratory shelf. The drunkard's search name comes from a well known joke, given here as I first heard it.
Someone sees a drunk man searching under a street light and asks him what he's looking for. He says he dropped his car keys; so, the stranger starts searching, also. After a while, the stranger asks the drunkard if he remembers the approximate location where he dropped them. The drunkard points at a car in the distance and says, "At my car." The confused stranger asks, "Then why are you looking here?" To which the drunkard replies, "The light's better."There are some other things in science that relate to alcohol. I'll lead with the lame joke that's likely funny only to middle school science students. A neutron walks into a bar and asks the bartender the price of a drink. The bartender replies, "For you, no charge." An alcoholic beverage actually assisted in an invention worthy of the Nobel Prize in Physics. Physicist, Don Glaser (1926-2013) used beer in experiments to create the bubble chamber used in early particle physics experiments. Movement of charged particles through a liquid just below its boiling point creates an ionization track that vaporizes the liquid to form microscopic bubbles. This beer story has been told as Glaser's being inspired by observing a glass of beer he was drinking, but he said that this wasn't the case.

(Scan of my copy. Click for larger image.)
Nobel Physics Laureate, Richard Feynman (1918-1988) decided to refrain from alcohol when he realized that he might become addicted to it.
As he wrote in his autobiography, "Surely you're joking, Mr. Feynman,[3] "I started to walk into the bar, and I suddenly thought to myself, "Wait a minute! It's the middle of the afternoon. There's nobody here. There's no social reason to drink. Why do you have such a terribly strong feeling that you have to have a drink?" - and I got scared. I never drank ever again, since then. I suppose I really wasn't in any danger, because I found it very easy to stop. But that strong feeling that I didn't understand frightened me. You see, I get such fun out of thinking that I don't want to destroy this most pleasant machine that makes life such a big kick."
References:
- Stumblebum (n.) at etymonline.com.
- My somewhat old desktop computer has an Intel dual core i3-4160 64-bit CPU running at 3.6 GHz with 8 GB of memory. The Linux operating system runs the 5.15.0-73-generic x86_64 kernel with a Cinnamon 5.4.12 desktop on Linux Mint 21.
- Richard P. Feynman and Ralph Leighton, "Surely You're Joking, Mr. Feynman!": Adventures of a Curious Character, W. W. Norton & Company; Reissue edition (February 6, 2018), Paperback, 400 pp., ISBN: 978-0393355628 (via Amazon).