
Palindrome Numbers
January 31, 2022 Desk Set is an enjoyable 1957 film directed by Walter Lang and staring Spencer Tracy and Katharine Hepburn. The plot of this film is based on a fanciful depiction of mainframe computers and their operation in the late 1950s. This computer, called EMARAC (for Electromagnetic Memory and Research Arithmetical Calculator), could do natural language processing, and it had a database that's equivalent to the Internet of today. Tracy is portrayed as a methods engineer, but he actually plays something like a computer scientist who's been assigned to computerize a library. Employees resist deployment of the computer, since they believe that it's intended to replace them, but that didn't happen. The film acknowledges the assistance of the International Business Machines Corporation in its production, and some critics have called the film an IBM propaganda piece with the message that computers won't take your job. For no apparent reason, Tracy gives Hepburn an IQ test during a luncheon meeting. Their conversation features two palindromes. Palindromes are a word or phrase that's the same whether read forwards or backwards. One is Adam's supposed first words to Eve, Madam, I'm Adam. The other is something Napoleon might have said, Able was I ere I saw Elba, Elba being the place of Napoleon's first exile from 1814 to 1815. It's not surprising that there are an infinite number of palindromic numbers, and creating such numbers is all too easy. It's more fun finding prime numbers that are also palindromes. These palindrome primes are integer sequence A002385 of the On-Line Encyclopedia of Integer Sequences. A simple example is the number eleven; a more complex one is 17471. Palindromic primes are found in number bases other than base 10 (decimal). The prime number 1991 is also a palindrome when written in hexadecimal, 7C7. Just below one million (which is obviously not a palindrome) we have 98689 as a palindrome prime; or, the hexadecimal palindrome prime F383F (997439 in decimal). These are very easily generated in a high-level language, and my PHP and C language programs to calculate palindrome primes can be found here.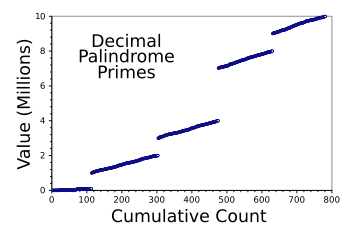
graph of decimal palindrome primes less than ten million.
There are 781 decimal palindrome primes up to 9,989,899.
The gaps are a consequence of the fact that every palindrome with an even number of digits is divisible by 11, so these numbers are not prime.
(Data from my C language program, graphed using Gnumeric. Click for larger image.)
After discovering a mathematical concept, mathematicians search for possible variants. Such is the case for the Pythagorean theorem, for which there are more than 370 proofs.[2] My favorite, perhaps because of its simplicity, is shown figure. It's credited to the 12th century Hindu mathematician, Bhaskara (1114-1185). One proof, thought to have been created by Leonardo da Vinci (1452-1519), was actually authored in 1772 by German physicist, Johannes Tobias Mayer (1752-1830).[3]
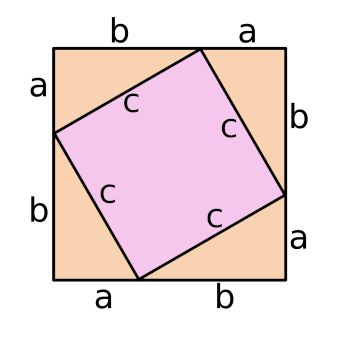
A proof of the Pythagorean theorem by Bhaskara.
In Bhaskara's proof, the area of the inner square is c2, the area of the outer square is (a+b)2, and the area of each triangle is (1/2)(ab).
U.S. President, James Garfield (1831-1881), created a novel proof when he was a member of the U.S. House of Representatives. His proof equates the area of a trapezoid to the combined area of its contained triangles.
(Drawing by the author using Inkscape. Click for larger image.)
Mathematician, Daniel Tsai, has examined a variant of palindrome numbers that he calls v-palindromes.[4] The numbers themselves are not palindromes; rather, the palindrome property arises from the fact that these numbers and the numbers formed by reversing their digits have the same sum of their factors. For example,
198 = 2 · 3 · 2 · 11Tsai writes that he first discovered his v-palindromes in 2007, when he was just 15 years old.[4] His first publication on the topic was in October, 2018, in Sṓgaku Seminar magazine, which he describes as the American Mathematical Monthly of Japan.[5] This paper also proved that there are infinitely many v-palindromes in base ten.[4] This is a simple proof in which it is shown that numbers with any number of nines in the middle, are v-palindromes in base ten (e.g., 18, 198, 1998).[4] Furthermore, all numbers with any number of 18's repeatedly concatenated are v-palindromes in base ten (e.g., 18, 1818, 181818).[4]
2 + 3 + 2 + 11 = 18
891 = 3 · 4 · 11
3 + 4 + 11 = 18
| Number Base | Smallest v-palindrome (decimal equivalent) |
|---|---|
| 2 | 175 |
| 3 | 1280 |
| 4 | 6 |
| 5 | 288 |
| 6 | 10 |
| 7 | 731 |
| 8 | 14 |
| 9 | 93 |
| 10 | 18 |
| 11 | 135 |
| 12 | 22 |
| 13 | 63 |
| 14 | 26 |
| 15 | 291 |
| 16 | 109 |
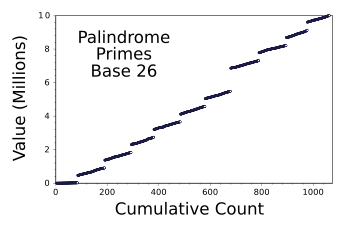
Graph of hexavigesimal (Base 26) palindrome primes less than ten million.
There are 1062 hexavigesimal palindrome primes up to 9998633 (lmmml).
(Data from my C language program, graphed using Gnumeric. Click for larger image.)
References:
- Desk Set (1957) Walter Lang, Director, on the Internet Movie Database.
- Elisha Scott Loomis, "The Pythagorean proposition: its demonstrations analyzed and classified, and bibliography of sources for data of the four kinds of proofs," Education Resources Information Center. Institute of Education Sciences (IES) of the U.S. Department of Education (1940); reprinted in 1968 by National Council of Teachers of Mathematics (310 page PDF File).
- Franz Lemmermeyer, "On Leonardo da Vinci's proof of the Theorem of Pythagoras," arXiv, January 15, 2014.
- Daniel Tsai, "v-palindromes: an analogy to the palindromes," arXiv, November 17, 2021.
- Tsai, D. (2018). Natural numbers satisfying an unusual property. Sṓgaku Seminar, vol. 57, no. 11), pp. 35-36 (in Japanese).