
A Special Triangle Pair
June 1, 2020 When scientists write for publication, they're very careful with the text. Multiple drafts are circulated among coauthors to ensure that all the results are included and nothing is ambiguous. There's also adherence to some questionable style requirements such as writing in an active voice, rather than a passive voice. I've always preferred the passive voice and the editorial we, but most grammarians object to these. Things are different when scientists read a paper. They ignore the text and go right to the figures. The adage, "A picture is worth a thousand words," is as true today as a century ago, as is the logical consequence that "1001 words is worth more than a picture."[1] Fortunately for English speakers, most science is written in English, but papers in other languages can be understood just by their figures. There are multiple ways to present data, some better than others. Edward Tufte (b. 1942) is an acknowledged expert in informational graphics.[2] Tufte is also a hero of self-published authors, since he self-published a commercially successful book, "Visual Display," by taking out a second mortgage on his home. This was in 1982, before the self-publishing boom caused by the Internet. Today, self-published authors have a much lower financial barrier. Tufte was an early critic of the way that Microsoft PowerPoint is used to present information at meetings. Tufte prefers written reports to PowerPoint, but I still find PowerPoint (in my case, LibreOffice Impress) to be effective.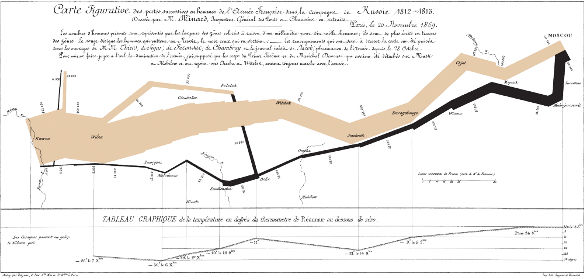
An 1869 chart by Charles Minard (1781-1870) depicting Napoleon's 1812 Russian Campaign. The majority of articles about informational graphics contain this figure. This chart combines data on the number of men in Napoleon's men, their movements, as well as the temperature they encountered on the return path. This chart quite effectively represents the army losses.(Via Wikimedia Commons. Click for larger image.)
I thought about information graphics when I was doing some experimental mathematics on an interesting pair of triangles. I was introduced to these triangles by a posting on Evelyn Lamb's Roots of Unity blog.[3] She writes that there is only one pair of triangles, one right triangle and one isosceles triangle, that have integer side length, equal perimeters and equal areas (see figure). Lamb gives some background on this problem, which relates to algebraic geometry.[3]

A right triangle and an isosceles triangle with the same perimeter and area.
In each case, the perimeter is 864, and the area is 23,760.
(Created using Inkscape)
I decided to examine the area of all triangles with the same perimeter intermediate between these two triangles; that is, I examined all triangles with sides a = [132..135], b = [352..366], c = [366..377], selected those with perimeter 864, and calculated their areas. There are 46 triangles that meet the perimeter criterion, and these were discovered with a simple computer program (source code here, and the resultant data file here). Finding the area is easy if you know the height (altitude) of the triangle, since the area is given by the formula A = (1/2)bh in which b is the length of the base, and h is the height. In this case, in which the height is unknown, it's easier to use Heron's formula,
Where s, a parameter known as the semiperimeter, is half the perimeter; viz.,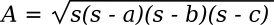
This equation can be written in terms of the sides, only, as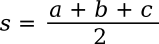
As a first visualization, I wrote a computer program that created an SVG image of all the triangles (source code here, and a required data file of apex data is here). Drawing the triangles required a calculation of the positions of the three apices of each triangle. This was done using the Gnumeric spreadsheet application. While two of these apices are trivial, since they are at the ends of the base, one of them is at the top of the triangle altitude. A little bit of algebra using the Pythagorean theorem found that h2 = b2 - (a-x)2, and h2 = c2 - x2, where x is the location of the altitude on the base. Solving these equation for x gives us the x-position and the y-position of the final apex, and it allowed generation of this figure.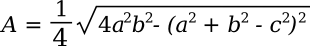
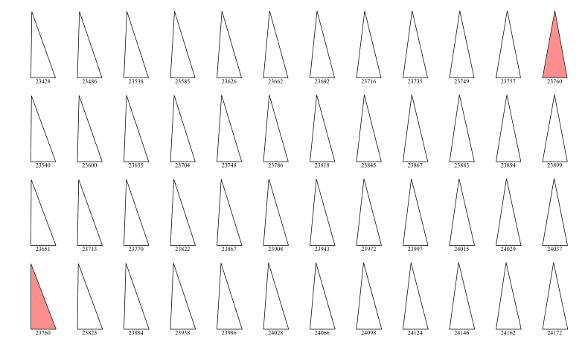
Triangles with a perimeter of 864 with sides in the range of a = [132..135], b = [352..366], and c = [366..377]. The special pair of triangles is shown in red. (Generated by a computer program, as explained in the text. Click for larger image.)
So, how does the area vary over these triangles? Although the data could be presented as a table, the table would have 48 rows, and it would be difficult to discern any patterns. That's why informational graphics are important. I tried various ways of graphing the data, and I decided that the column chart, shown below, is the most informative. It's also aesthetically pleasing, and the pattern is reminiscent of the reflectors of a Yagi antenna.
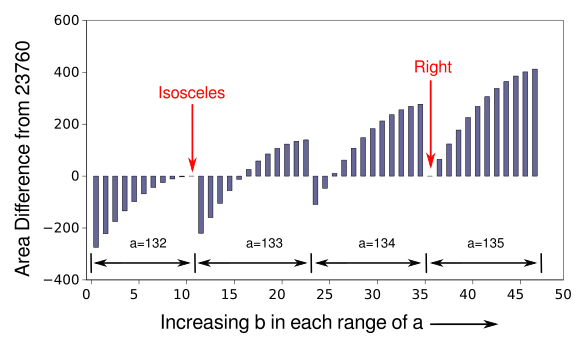
Column chart of the area data, as sorted in increasing a, then b, values. Since the differences in area are small with respect to the average area, the differences from the "ideal" area are shown. The locations of the isosceles and right triangles are shown. (Click for larger image.)
I tried several other graph types. The radial and surface graphs, shown below, don't provide as much information. The radial graph is interesting from an artistic perspective, and it makes me wonder how much good art might be lurking in mathematical problems like this.
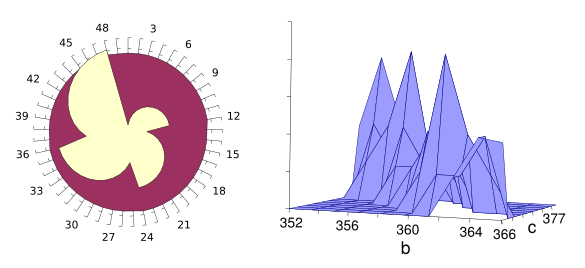
Like a dove. On the left is a radial plot of the area data, looking very much like a dove. On the left is a surface plot of the area in terms of side lengths b and c.
Mathematics has enriched art through such concepts as perspective, and many artists have created geometrical works. One example is Josef Albers (1888-1976), who created a series of paintings called "Homage to the Square." (Both plots rendered using Gnumeric.)
I decided to find how close a triangle could come to the area of an equilateral triangle with sides 200 and perimeter 600. I checked all triangles with sides a = [180..220], b = [180..220], and c = [180..220]. A triangle with sides 188-211-203 comes within −0.000890% of the 17320.508076 area of the equilateral triangle. Alas, the perimeter of this triangle is 602.