Tikalon Blog by Dev Gualtieri

Educated Guessing

December 7, 2020

Knowledge comes from experiment, but the results of most experiments are not as definitive as one would like. While most physical scientists are able to control their experiments quite closely, and chemists will choose pure materials for their reactions, there are oservational errors and instrument calibration errors, and variation in room temperature and pressure, and humidity from one day to another.

Likewise, experiments in many of the life sciences are conducted on organisms that are not precisely equivalent from one individual to another. Fortunately, the powerful analysis tools of statistics and regression analysis can coax a reasonable result from experimental data. Statistical analysis benefits from many observations, since the deviation from the mean value scales as the square root of the number of measured values, so experiments benefit from multiple trials.

Statistics has allowed science to extract knowledge from data, but it has also been used to extract knowledge from opinion, as demonstrated in 1906 by the Victorian polymath, Francis Galton (1822-1911).[1] Galton observed a contest at a livestock fair in which 787 visitors guessed the weight of a particular ox.[2]

People in attendance at a livestock fair a hundred years ago would have had a reasonable knowledge of the weight of oxen, but they would be unlikely to guess the exact weight. While there was a wide range of estimates, the mean of the 787 guesses, 1197 pounds, was within a pound of the actual weight of 1,198 pounds; that is, the mean was within 0.1% of the actual value.[2] This phenomenon is called the "Wisdom of the Crowd."

A fat 3-year old heifer (Wellcome Trust image V0021653)

A fat, 3 year old heifer, shown in an etching by T. Hatton.

While Galton's ox was a hefty 1,198 pounds, the average weight of cattle in the United States is presently about 1370 pounds.[3]

(Wellcome Trust image V0021653 (modified), via Wikimedia Commons

Statistics are not robust against bad data, so scientists take great care in designing experiments that give data relatively free from interfering variables. Some will do computer modeling to determine that things are controlled enough to produce good data, but everything usually starts with some back-of-the-envelope calculations. One of the most common of these in solid state physics is calculating what vacuum pressure is required in a chamber to prevent contamination of a cooled surface with gas molecules over the course of an experiment. If you can't achieve that requirement, you shouldn't even attempt your experiment.

Scientists sometimes venture out of their laboratories, but they use their ability to do quick back-of-the-envelope calculations to make educated guesses about things in the outside world. A master of this was 1938 Physics Nobel Laureate, Enrico Fermi (1901-1954), who was famous for posing, and also solving, what are called "Fermi problems." These are estimates of unusual quantities based on whatever information is at hand.

Enrico Fermi at a laboratory control panel.

Enrico Fermi (1901-1954 at a laboratory control panel, sometime between 1943 and 1949.

Chemical element 100, Fermium (Fm), is named in his honor. It was discovered in 1952 at Lawrence Berkeley National Laboratory while Fermi was still living, although not officially called Fermium at the time.

There's an amazingly long list of things named after Fermi.

(Portion of a Wikimedia Commons image from the National Archives and Records Administration, NAID 558578.)

One example of a Fermi problem that I described in an earlier article (Estimation, December 21, 2011) is his calculation of the number of piano tuners in Chicago. This estimate involves quantities such as the fraction of households that have pianos (many more at the time of the calculation than today), how often they are tuned, and how long it takes to tune a piano. I would often make similar estimates, such as the population of our county, based on the number of supermarkets.

Another example was Fermi's estimate of the yield from the Trinity nuclear test. This was the first detonation of a nuclear weapon. Years earlier, Edward Teller (1908-2003) had the idea that this detonation might cause a runaway fusion of atmospheric nitrogen; that is, set the atmosphere on fire and destroy life on Earth.[4] Hans Bethe (1906-2005) did a calculation that showed that this was impossible. Fermi, probably to relieve the psychological stress at Trinity, proposed bets on whether this would happen.[4] Fermi's yield test was based on how far pieces of paper were blown by the pressure wave of the blast. His back-of-the-envelope calculation, which in this case may have actually involved a shredded envelope as the source of the bits of paper, gave a value about half the actual value of 22 kilotons of TNT.

Perhaps the most adventuresome of such calculations is the Drake equation that estimates the number of detectable extraterrestrial civilizations in our Milky Way galaxy. This 1961 equation by radio astronomer, Frank Drake (b. 1930), has seven estimated quantities that are multiplied together to give the number of such civilizations. While the logic behind this equation is sensible, the uncertainty in these seven terms is such that the equation leads to a wide range of possible values.

Radio astronomer Frank Drake speaking at Cornell University (Ithaca, New York), October 19, 2017.

Drake and Carl Sagan (1934-1996) designed the Pioneer plaque in 1972. This plaque was designed to provide information about Earth and its inhabitants to any extraterrestrials who might discover the spacecraft.

Drake also supervised creation of the Voyager Golden Record, a more elaborate message than the Pioneer plaque.

(Portion of a Wikimedia Commons image by Amalex5.)

A back-of-the-envelope calculation of the number of workers involved in the construction of the Great Pyramid of Giza, was presented by Vaclav Smil in a recent issue of IEEE Spectrum.[5] This pyramid, built in a period of 10-20 years around 2560 BC, was created from 2,500,000 cubic meters (91,000,000 cubic feet) of limestone and granite. Using some basic physics, Smil estimates that the number of workers involved was far fewer than commonly believed.

The only historical account of the number of workers was that of the Greek historian, Herodotus (484- c.425 BC), who wrote about the topic about two millennia after the fact in The Histories.[6] In 1974, physicist, Kurt Mendelssohn, estimated a labor force of 70,000 seasonal workers with perhaps as many as 10,000 permanent masons.[5] Smil's estimate from some first principles thermodynamics yields a much smaller workforce.

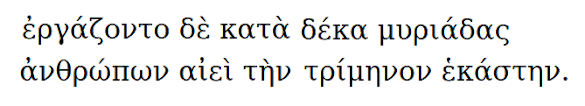
Herodotus, The Histories, Book 2, Section 120, Euterpe

The portion of The Histories (Book 2, Section 120, Euterpe) by Herodotus describing the workforce for building the Great Pyramid of Giza. It reads in translation that "A hundred thousand men laboured constantly, and were relieved every three months by a fresh lot." (Greek text and translation from Sacred Texts.[7])

Smil considers the potential energy required to lift all that stonework to its proper level, a simple calculation involving gravitational acceleration, the density of the stone (about 2.6 g/cc), and the center of mass of the pyramid, which is at one-quarter its height.[5] He balances this energy (about 2.4 trillion joules) against the useful work that can be extracted from the basal metabolic rate of a human (about 450 kilojoules a day).[5]

This gives 5.3 million man-days for raising the pyramid, or about 18,000 man-years. If the construction took 20 years, the workforce to raise the pyramid is only about 900 men.[5] Others would have been needed to quarry the stone, move it into place, oversee the details of construction, and provide other support functions. Smil's total estimate is fewer than 7,000 workers, an order of magnitude fewer than previously thought.[5]

The Great Pyramid of Giza of one of the Seven Wonders of the Ancient World, a list that included the Statue of Zeus at Olympia and the Lighthouse of Alexandria.

The list also included the Hanging Gardens of Babylon, the existence of which is disputed. They are not mentioned in any extant Babylonian manuscripts, and there is no archaeological evidence for their existence. This is quite unexpected, since the gardens were supposedly created nearly 2,000 years after the Great Pyramid of Giza.

(Wikimedia Commons image by Alex lbh)

I've done my own calculation of an historical event by calculating the number of warriors who fought in the Trojan War, the best record of which is Homer's Iliad. The Catalog of Ships in Book II of the Iliad lists 1186 ships. The Greek troop transport of that era had 22 rows of paired oarsmen, for 44 men per ship. This gives 52,184 men. We could give allowances for the nobility, who likely did not row, to round this up to about 53,000. Some scholars have inflated this figure upwards to 100,000-135,000, but I believe they were using the plan of a much later Greek warship that held more men.

It appears that the Trojans were outnumbered more than 10:1, as indicated in Book II, ll. 125-134, which in Alexander Pope's translation reads,

"So small their number, that if wars were ceased,
And Greece triumphant held a general feast,
All rank'd by tens, whole decades when they dine
Must want a Trojan slave to pour the wine."

This means that if there were Trojans assigned to pour wine for groups of ten Greeks, there would be some Greeks without a server. Some of these servers would have been women, so there may have been perhaps 3,000 Trojan warriors. This leads to my estimate of the number of warriors in the Trojan War as 53,000 + 3,000 = 56,000.

Educated Guessing

References: