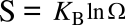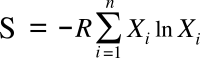Tikalon Blog by Dev Gualtieri

Ductile High-Entropy Alloys

February 25, 2019

It's playtime at the elementary school, and the teacher marches her children outside to the playground. There are rules of decorum inside the school, and all the children have learned to march in a single file out the door. Once out the door, it's the usual chaos at the playground until the teacher signals that it's time to return to the classroom, The children queue at the door for their march back to class. Their arrangement, however, is not the same as when they arrived. That's an example of entropy.

While the idea of entropy was known from Carnot's 1824 work on the efficiency of heat engines, now codified in the second law of thermodynamics, it was given a statistical interpretation by Ludwig Boltzmann (1844-1906) around 1875. Boltzmann's entropy formula is easily written:

where S is the configurational entropy, K_B is Boltzmann's constant of 1.38065 x 10²³ joule/kelvin (J/K), and Ω is the number of states accessible to a system; that is, the ways in which atoms can be differently arranged.

Austrian physicist, Ludwig Boltzmann (1844-1906), in a 1902 photo.

As Seneca the Younger (c. 4 BC - 65 AD) quoted Aristotle in his De Tranquillitate Animi (On Tranquility of the Mind),[1] "No great genius has existed without an element of madness (Nullum magnum ingenium sine mixtura dementiae fuit)," and Boltzmann was an example of this.

Boltzmann appears to have been a manic depressive, with intense work in physics interrupted by periods of depression. This condition was exacerbated by the rejection of his ideas by his physics peers. He committed suicide in 1906 while on holiday with his family.

(Wikimedia Commons image, modified for artistic effect.)

If we form a crystal of a pure element, there's no entropy involved, since all the atoms are the same. Elements have isotopes that make some atoms distinguishable from others, but such isotopes behave identically as far as chemistry is concerned. In the case of combining atoms of i different elements of mole fractions X_i, the entropy is easily calculated:

where R is the gas constant of 8.314 joule/kelvin/mol. While we can imagine such a crystal forming with the different atoms populating the regular lattice sites in a crystal structure, it's the nature of atoms that they prefer to bond together in different ways. That's why a mixture of metal atoms typically results in a solid of different polycrystals. In most cases, formation of secondary phases is encouraged by the addition of certain elements to provide additional strength. That's why pure iron is soft, but iron with the addition of carbon forms steel strengthened by an iron-carbide phase (cementite).

Alloy design has always been about the creation secondary phases in a base metal to improve physical properties such as strength, fracture toughness, and ductility, and also chemical properties such as oxidation resistance and corrosion resistance. That mindset was broken with the 2004 publication by scientists at the Oxford University Department of Materials of a single phase alloy made from equal portions of five components.[2] This alloy was Fe₂₀Cr₂₀Mn₂₀Ni₂₀Co₂₀, which forms a face-centered cubic solid solution. The entropy of such a material is high, since the five different atom types can be distributed in many arrangements. Alloys of this type are called high-entropy alloys (HEAs).

Atomic structure model of the Oxford University FeCrMnNiCo alloy.

In this image, magenta = Fe, green = Co, blue = Cr, cyan = Ni, and yellow = Mn. Aside from slight differences in atomic size, swapping colors would serve just as well, since the composition is equi-atomic.

(Image by Shaoqing Wang, via Wikimedia Commons.)

Aside from being a thermodynamic curiosity, do HEAs have any beneficial properties? Equi-atomic multicomponent alloys have good resistance to radiation damage, since they are more tolerant to having their atoms displaced by energetic particles such as neutrons. It's been observed that HEAs with the body-centered cubic crystal structure have high strength and low ductility, while the converse is true for face-centered cubic HEAs; however, the statistical sample size is too small at this time to call this a rule.

A recent paper by Chinese scientists presents their research on the cryogenic ductility of the face-centered cubic high-entropy alloy, Co Cr Fe Ni. As numerous YouTube videos of immersing various objects into liquid nitrogen have demonstrated, most materials become brittle (less ductile) at low temperatures. While most of these demonstrations are a cheat, since the objects contain water, this is a phenomenon that happens for some alloys. Certain steels will become brittle at temperatures below about -50 °C, and this was only discovered after many World War II "liberty ships" were lost in the cold waters of the North Atlantic Ocean.

We need ductile metals that sustain their fracture toughness at cryogenic temperatures for such applications as spacecraft and containment vessels for Superconducting magnets. A good target would be an ultimate tensile strength greater than 1 GPa, and a strain at fracture greater than 60%.[4] This is difficult at cryogenic temperatures in most alloys, since the motion of dislocations is limited.[3] The CoCrFeNi high-entropy alloy was demonstrated to have a strength of 1.25 GPa and a strain at fracture of as large as 62% at liquid helium temperature (4.2 K).[3-4]

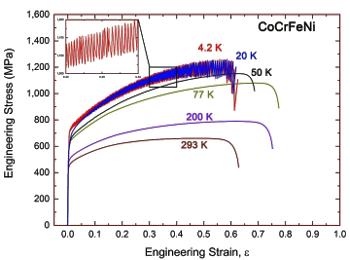
Tensile tests of the CoCrFeNi high-entropy alloy at different temperatures.

An interesting feature is the serration (saw tooth) feature that appears in the stress-strain curve.

Deformation twinning produces strain-hardening that sustains plastic flow at stresses, resulting in the serration feature.[3]

(Image © Science China Press.)

The researchers conjecture that the high strength and ductility of the alloys arises from the low stacking fault energy at extremely low temperatures and a resulting deformation twinning.[3]

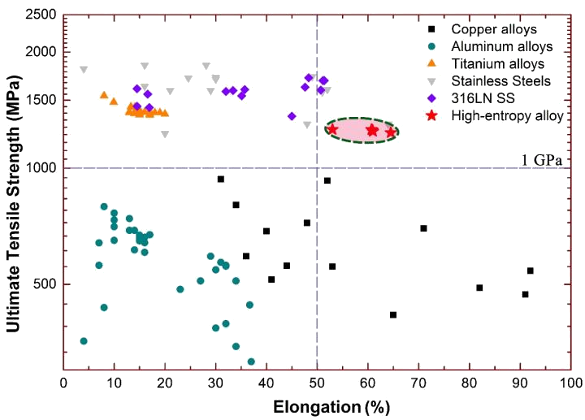
Ultimate tensile strength vs elongation for different materials at liquid helium temperature (4.2K). The CoCrFeNi high-entropy alloy shows superior properties. (Image © Science China Press.)

In a recent publication, the high entropy alloy concept has been extended to oxide ceramics containing equi-molar ratios of multiple transition metals and/or rare earth elements.[5] These oxides have been shown to exhibit a strong tendency to crystallize in simple single phase structures, as would be expected from the high degree of configurational entropy.[5] One studied high entropy oxide (HEO) was X(Co_0.2Cr_0.2Fe_0.2Mn_0.2Ni_0.2)O₃ in which X was Gd, La, Nd, Sm, or Y.[5]

Ductile High-Entropy Alloys

References: