
Euler on Divergent Series
September 17, 2018 Infinite series can bring great joy or great pain. They're wonderful when they converge, and converge rapidly, but they're a pain when they diverge. My first introduction to the wonder that's an infinite series was in elementary school. I had done many trigonometry homework problems using trig tables, and I had always thought that these tables were created by expert draftsmen with precise protractors and rulers. It was obvious that they would draw huge triangles on their drawing boards, measure the sides and angles very carefully, and then calculate the sine, cosine and tangent values.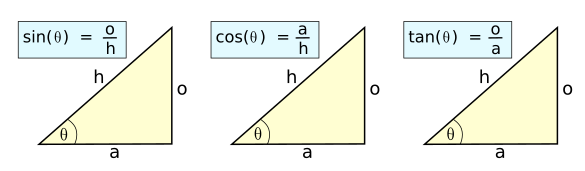
I attended elementary school in Upstate New York, the locale of several indigenous Indian tribes that included the Oneidas, Onondagas, and Mohawks, all of whom were part of the Iroquois Nation. We were taught to remember the trigonometric functions using the mnemonic of an Indian princess named "Sohcahtoa." (Created using Inkscape. Click for larger image.)
How surprised I was when I found that these tables were calculated to great precision using the infinite series expansions given below. While mathematicians are typically less prone to exaggeration than scientists, they did decide to use an exclamation point to signify a factorial number. The patterns for the sine and cosine functions are easy to see, but the one for the tangent function is somewhat obtuse (pun intended).
In these functions, the angle x is in radians. While the sine and cosine series are valid for any value of x, the x-values for the tangent function are restricted to values between -π/2 to π/2, since the tangent is infinity at 90-degrees. There's also an infinite series representation of e, the base of the natural logarithms, as follows,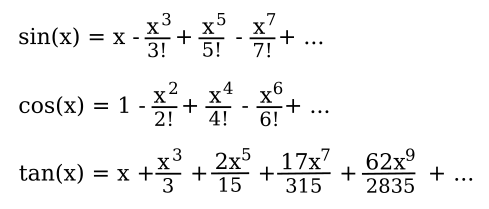
This fact, coupled with the very strange imaginary unit, i, which is the square-root of negative one (√-1), gives some other trigonometric identities, cos(x) = (eix + e-ix)/2, sin(x) = (eix - e-ix)/2i, and tan(x) = (1/i)(eix - e-ix)/(eix + e-ix). Playing with such series allowed the famous Swiss mathematician, Leonhard Euler (707-1783), to devise what's called Euler's formula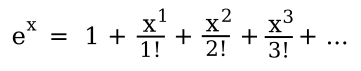
which gives us what's called Euler's identity when evaluated at x = π,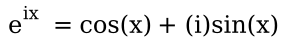
This combines five interesting mathematical constants, 0, 1, e, i, and π, into one equation.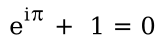

A 1753 pastel portrait of Leonhard Euler by Jakob Emanuel Handmann (1718–1781).
Perhaps keeping his brain warm was one trick that Euler used to create his mathematics, although scientific evidence indicates that people think better when cooler.
(Photograph of a portrait at the Kunstmuseum Basel, via Wikimedia Commons)
Euler was a voluminous author, as the Euler Archive on the Mathematical Association of America website will attest.[1] Alexander Aycock, once at the Institute of Physics of the Johannes Gutenberg-Universität Mainz, has published on arXiv many translations of Euler's papers from Latin into English. He recently published a translation of Euler manuscript (Eneström-Number, E247), "De seriebus divergentibus (On divergent series)."[1] Euler's paper was presented at the French Academy of Sciences in 1746, and it was published in 1760. Not all series will sum to a finite results. The series that sum to infinity are called divergent, and it's not always easy to determine whether or not a series will diverge. Lest you think that a series for which the successive terms grow smaller and smaller, becoming zero at infinity, will necessarily converge, there's the example of the harmonic series
1 + 1/2 + 1/3 + 1/4 + 1/5 + 1/6 + 1/7 + ...In this series the last term would be zero, but the harmonic series sums to infinity, a fact first deduced by Nicole Oresme (c.1320-1382), a polymath of the Middle Ages. One simple proof of the divergence of the harmonic series is to consider, instead, the similar series in which elements of the harmonic series are systematically replaced by smaller values, that should sum to a smaller value,
1 + 1/2 + 1/4 + 1/4 + 1/8 + 1/8 + 1/8 + 1/8 + 1/16 + 1/16 + ...by doing partial sums in this series, we get the equivalent and obviously divergent series,
1 + 1/2 + 1/2 + 1/2 + 1/2 ...
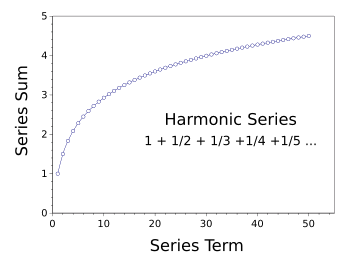
Sum of the harmonic series up to the fiftieth term.
Looks divergent to me, but mathematical rigor demands more than a feeling.
(Created using Gnumeric)
The first part of Euler's manuscript on divergent series deals with Grandi's_series, which is simply
1 - 1 + 1 - 1 + 1 - 1 + 1 - 1 + ...This series is interesting enough to have been considered by many mathematicians, including such luminaries as Gottfried Wilhelm Leibniz (1646-1716), Jacob Bernoulli (1654–1705), Daniel Bernoulli (1700-1782), Jacopo Francesco Riccati (1676-1754), Joseph-Louis Lagrange (1736-1813), Augustus De Morgan (1806-1871), and Ferdinand Georg Frobenius (1849–1917).
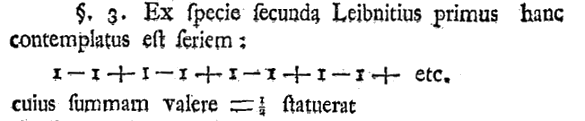
Portion of Euler's "De seriebus divergentibus" that discusses Leibniz's analysis of what is now called Grandi's_series. The English translation reads, "From the second species, Leibniz at first considered this series, 1 − 1 + 1 − 1 + 1 − 1 + 1 − 1 + etc., the sum of which he stated to be = 1/2..." (From The Euler Archive Website of the The Mathematical Association of America.[2-3])
One obvious method of analysis of this series is to use the partial sums method we used on the harmonic series. Thus, we can group the series elements as follows;
(1 - 1) + (1 - 1) + (1 - 1) + (1 - 1) + ...to give us zero. But, what if we group the elements as follows
1 + (-1 + 1) + (-1 + 1) + (-1 + 1) + (-1 + 1) ...which gives a sum of one. So, which is it, one or zero? Leibniz, in an analysis that was more philosophical than mathematical, decided to split the difference, and he wrote that the series sums to 1/2 (as revealed in the excerpt of Euler's manuscript shown above). We can get 1/2 as well by a proper grouping and an algebraic manipulation of the sum S,
S = 1 + (-1 + 1) + (-1 + 1) + (-1 + 1) + (-1 + 1) ...Euler notes that the series expansion of the algebraic fraction, 1/(1+a), will yield Grandi's_series when a = 1.
1- S = 1 − (1 − 1 + 1 − 1 + ...) = 1 − 1 + 1 − 1 + ... = S
1- S = S
1 = 2S
S = 1/2
and this series has a residual, the value remaining after summing a finite number of terms, as follows: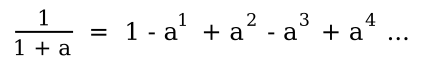
This residual is non-zero, so it can't be ignored when n is infinity. After remarking that the objection might be made that there really isn't an infinite term, Euler did another analysis using finite differences in what's now called the Euler transform to get the same 1/2 that Leibniz claimed. At this point, there is no consensus on the sum of this series.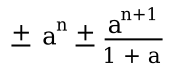
References:
- The Euler Archive, The Mathematical Association of America
- L. Euler, "De seriebus divergentibus“, Novi Commentarii academiae scientiarum Petropolitanae vol. 5, no. 1760 (1760), pp. 205-237, Latin PDF File.
- Alexander Aycock, Translation of Euler's "On divergent Series," arXiv, July 31, 2018.
- Euler's "On divergent Series," English Translation at the Johannes Gutenberg-Universität Mainz Website.