Tikalon Blog by Dev Gualtieri

Twice Broken Sticks

July 2, 2018

If you ask people to name the most popular book of 19th century America, many might name Herman Melville's 1851 novel, Moby-Dick, more properly Moby-Dick; or, The Whale. While this book is often hailed as one of the Great American Novels, it did not sell well in its time. Moby-Dick sold just a few thousand copies, with Melville earning just a little over a thousand dollars for his effort, which is about $20,000 in today's money.

The actual best selling American book of that century (behind the Bible) was Uncle Tom's Cabin by Harriet Beecher Stowe (1811-1896) which sold 300,000 copies in the United States and a million copies in Great Britain in the first year of its publication in 1852. Another best seller was Mark Twain's 1884 Adventures of Huckleberry Finn.

However, the best non-fiction work of that century was the Personal Memoirs of Ulysses S. Grant, written by the 18th President of the United States, Ulysses S. Grant (1822-1885), who had served as the 6th Commanding General of the United States Army during the American Civil War (1861-1865). This book was published by Mark Twain in the year of Grant's death.

Grant's principal purpose in writing his memoirs was to provide for his family after being diagnosed with terminal throat cancer that was the likely consequence of a voracious cigar and whiskey habit. Abraham Lincoln, when cautioned about Grant's drinking problem, supposedly requested the name of his favorite whiskey, so he could send a barrel to each of his generals.[1]

Motivated by his rapidly declining health, Grant wrote up to fifty pages a day and finished the manuscript five days before his death. Twain made a considerable profit on Grant's memoirs, which sold hundreds of thousands of copies, but he subsequently lost millions of dollars in today's money on his investment in the Paige Compositor, an early typesetting machine.

Gaius Julius Caesar (100 BC - 44 BC) (left) and Ulysses S. Grant (1822-1885) (right). (Left image, a bust of Caesar from the 1902 book, History of the World, edited by H. F. Helmolt, from Wikimedia Commons, courtesy of The General Libraries, the University of Texas at Austin. Right image, a portrait of Grant taken sometime between 1855 and 1865, from the Library of Congress, American Memory Collection, Digital ID, cwpb 06971, via Wikimedia Commons.)

Grant's memoirs were in a long tradition of military memoirs that date back to at least the time of Gaius Julius Caesar (100 BC - 44 BC). Caesar wrote his account of the nine-year Gallic Wars (58 BC - 50 BC) as a third-person narrative in the well known book, Commentarii de Bello Gallico.[2] This book is familiar to students of Latin, since its simple grammar is quite accessible and used to teach the language. The famous first line of the book, "Gallia est omnis divisa in partes tres" ("Gaul is a whole divided into three parts"), is still remembered by those students after decades.

Physicists and mathematicians have had a long history of things broken into three parts. As I described in a previous article (Spaghetti in Physics and Math, January 7, 2011), Physics Nobelist, Richard Feynman, noticed that when you bend a strand of dry spaghetti beyond a critical bend radius, it breaks, not into two pieces, but three and sometimes more.[3]

Although Feynman experimented with dry spaghetti in an attempt to explain this effect, his wasn't able to discern its extremely subtle cause. After the first fracture, into two pieces when the bend radius is exceeded, a flexural wave travels down the broken pieces to cause subsequent fractures. All this was revealed by high speed photography.[4-5]

A spaghetti problem in the realm of mathematics involves a dry spaghetti strand broken into three random lengths. This problem, conceived as far back as 1854, asks the probability that these three pieces can form a triangle.[6] It's quite apparent that you can only build a triangle when the sum of the lengths of any two sides exceeds the length of the third side, a condition known as the triangle inequality (see figure).

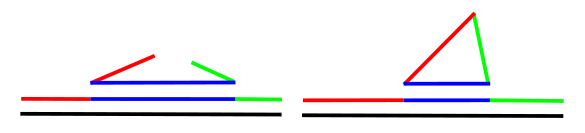
Building a triangle from a broken strand of dry spaghetti, or from a broken stick. (Created using Inkscape)

The probability that a stick broken into three random lengths can build a triangle is only 25%.[6-7] An analytical solution of this is given in ref. 6, and a Monte Carlo calculation to verify this is quite simple; so simple, in fact, that even I was able to create a very short computer program to do this (source code here). The histogram of successful triangle builds for 10,000 trials of 10,000 broken sticks appears below.

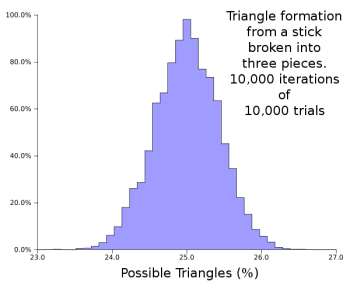
Histogram of 10,000 iterations of 10,000 trials for success in building a triangle from a stick broken into three pieces. (Click for larger image)

The saga of the twice broken stick continues, as evidenced by a recent paper on arXiv by Steven R. Finch, a mathematician at the Massachusetts Institute of Technology. In this paper, he calculates the median area for objects built from randomly broken sticks, not only for triangles, but for quadrilaterals as well. In the case of triangles, the median area is quite small. For a stick of unit length, the median area is just 0.031458...[8]

The above truncated decimal for the calculated median area belies the extreme precision of the calculation. Finch gives the actual value as 0.0314584607846627648007001...[8] I write this as an example of why you shouldn't be too satisfied with the results of your computer simulations.

As an example, I wrote a Monte Carlo simulation of this problem (source code here) that gives a good value on my desktop computer in a few minutes. My program is not that elegant, so more iterations could be done in a shorter time, but the precision of the computer results are a long way from an actual calculation (see figure).

Histograms of mean and median area calculations for random triangles

Histograms of mean and median area computations for random triangles. We can be fairly certain that the median area falls between 0.0313 and 0.0317, but this precision is far behind the value of 0.0314584607846627648007001... of an actual calculation. (Created using Gnumeric. Click for larger image).

Twice Broken Sticks

References: