
NIST Randomness Beacon
October 1, 2018 I've been interested in random numbers since high school, when I stumbled upon the famous RAND Corporation book of a million random numbers at a public library.[1] This collection of random numbers was based on a RAND study for the US Air Force, and the random numbers were generated using a physical noise source. This book wasn't the first book of random numbers. That milestone was "Random Sampling Numbers," created by English statistician, L.H.C. Tippett (1902-1985), in 1927. The physical noise source was described as a random frequency pulse generator. This noise source was likely based on Johnson-Nyquist noise, the voltage noise seen across any resistor at a temperature above absolute zero. The random numbers derived from this noise were subsequently whitened; that is, the data were manipulated to enhance randomness.[2] I built a single digit random number generator using electronic noise in the same week that the first men walked on the Moon. In my circuit, white noise modulated the frequency of an oscillator. In those days, the random pulse source was realized by a few transistors, although the digit display needed a few TTL integrated circuits. The digit display was a nixie tube, which is today a popular nostalgia item.[3]
As many digits of pi that I've memorized, displayed in nixie tubes. (Nixie digits by Hellbus, via Wikimedia Commons, spliced together using the GNU Image Manipulation Program. Click for larger image.)
One simple whitening method was invented by computer pioneer, John von Neumann (1903-1957). This von Neumann Whitening operates on a bitstream of ones and zeros. The method takes two successive bits at a time, and maps them to a random stream as follows: (0,1) → 0, (1,0) → 1, (0,0) → NULL, (1,1) → NULL, the NULL meaning that the result is ignored, and you move on to the next two bits of input data. As can be seen in the example below of a bitstream slightly biased to 1, this method discards a lot of bits. Recent methods produce better results.[4-5]
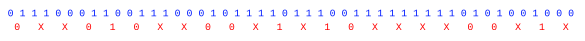
Von Neumann Whitening (randomness extractor) applied to a slightly biased random bitstream. (Drawn using Inkscape.)
One novel physical random number generator is a merger of art and algorithm called Lavarand in which random numbers are generated from images of active lava lamps. This physical random number generator had its own website hosted by Silicon Graphics in the late 1990s. The method is described in US Patent No. 5,732,138, "Method for seeding a pseudo-random number generator with a cryptographic hash of a digitization of a chaotic system."[6]
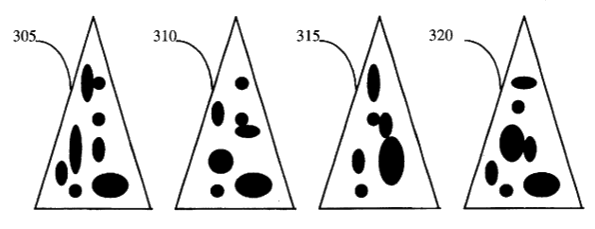
Figure three of the Lavarand patent.[6] (Via Google Patents.)
As Werner Heisenberg (1901-1976) realized as he developed his quantum uncertainty principle, quantum mechanics can be a source of exceptional randomness. As I described in a past article (Quantum Random Numbers, September 27, 2010), researchers at the Max Planck Institute for the Physics of Light (Max-Planck-Institut für die Physik des Lichts) have invented a quantum random number generator.[7] Their generator optically harvests randomness from the virtual processes in the quantum foam of the vacuum state. While carefully constructed physical noise generators will produce good random numbers, they're another piece of hardware that adds complexity to a system. That's why algorithmic random number generators, computer programs that generate random numbers, are usually preferred. The numbers that are generated by these are not strictly random; rather, they are just pseudorandom, since knowing the algorithm and its initial state allows the sequence to be reproduced exactly. As John von Neumann said in an obligatory quotation in any article on computer-generated random numbers,
"Any one who considers arithmetical methods of producing random digits is, of course, in a state of sin. For, as has been pointed out several times, there is no such thing as a random number - there are only methods to produce random numbers, and a strict arithmetic procedure of course is not such a method."The linear congruential generator is an extremely simple algorithmic random number generator that's based on recurrence relation published by D.H. Lehmer in 1948,
Xn = (aXn-1 + c) mod mWhen proper values are selected for a, c and m, this generator will produce a long sequence of random numbers. Computer scientist, Donald Knuth, noted that choosing a power of two for m simplifies the modulus operation, and he found good choices for a and c.
a=6364136223846793005, c=1442695040888963407, and m = 264.While such a random number generator is sufficient for computer simulation, a random number generator for cryptography requires more effort. The Mersenne Twister is based on the idea of the Mersenne primes.[8-9] It has a 32-bit implementation, called MT19937, based on the the 24th Mersenne prime, that has a period 219937 - 1. There is a 64-bit version called MT19937-64. The Mersenne Twister is used as the random number generator in Python, PHP, and some other programming languages. Source code for the Mersenne Twister is available at many places on the Internet, and my own C programming language implementation can be found here. Intermediate between the simplicity of the linear congruential generator and the Mersenne Twister is KISS, a simple generator that combines three different random number generators, a multiply-with-carry having a period of 2121 + 263-1, an XOR-shift of period 264-1, and a congruential generator of period 264.[10] KISS was written by George Marsaglia (1924-2011), an American mathematician and computer scientist who also assembled and published a suite of statistical tests of randomness known as Diehard.[11-12] I wrote a C programming language implementation of KISS, the source code of which can be found here. The program generates 100 million 64-bit random numbers, and it tests these for digit uniformity. A binary random number stream should contain as many zeros as ones, and the hexadecimal stream created by my program should have equal numbers of digits from 0 through F. Here's a list of the number of occurrences of each digit.
The standard deviation of these values is just 6465.770735, and the ratio of the standard deviation to the mean (100,000,000), called the coefficient of variation, is just 0.000065. The uniformity test is not infallible, since a repeated non-random string 0123456789ABCDEF would give ideal results. However, these numbers indicate a high degree of randomness for an actual random number generator. I mentioned earlier that Lavarand served random numbers on a website. With the availability of many random numbers at a keyboard's click on a desktop computer, is there any practical use for such an online service? If random numbers are used for such things as randomly selecting people for airport screening or randomly choosing members of a jury, using random numbers from a trusted public source will allay suspicions of bias.[13] Another use is proof that a document wasn't created earlier than a particular time. Still another use is as one input to a two-factor authentication system so that passwords for access to websites are effectively changed every minute.[13] That's why the National Institute of Standards and Technology (NIST) has launched a similar service called the NIST Randomness Beacon, and other countries are launching similar sites.[14-19] The NIST Randomness Beacon uses two commercially available and independent hardware entropy sources that are certified according to its own randomness standard, NIST SP 800-90A, "Recommendation for Random Number Generation Using Deterministic Random Bit Generators."[14] The numbers are subjected to a final whitening step.[17] The NIST Randomness Beacon serves a 512-bit random number every minute, together with a timestamp of its creation, and a hash with the previous value. The hash helps to maintain integrity against a retroactive change of a previous number.[14,17] There is also a full archive of all generated numbers. Not only does the Beacon provide numbers having excellent randomness, but these numbers are available to anyone who accesses the website.[14] The web site does have one caveat - The random numbers should not be used as cryptographic keys. It's not just the US that's interested in having a public source of timestamped random numbers. Chile is doing the the same with a generator that combines circuit noise with random data from things such as earthquake seismometer readings and radio streams.[17] The later noise source is reminiscent of the John Cage musical composition, "Symphony for Radios." Brazil has planned its own randomness beacon based on circuit noise and the statistics of radioactive decay.[17] All randomness beacons use the same data format, so it will be easy to combine these to make a new source of randomness.[17][0] = 100003299 [1] = 99992853 [2] = 99986788 [3] = 100002336 [4] = 99998079 [5] = 100003374 [6] = 99991133 [7] = 99992626 [8] = 100009032 [9] = 100007810 [A] = 100002324 [B] = 100001841 [C] = 100004021 [D] = 100001959 [E] = 100006852 [F] = 99995673
Example of the XML markup code output of the NIST Randomness Beacon. The very long hex numbers are truncated, and the UNIX timestamp translates to Tue, 24 Jul 2018 15:20:00 GMT. (NIST Randomness Beacon)
One problem with the NIST Randomness Beacon is that some cryptologists don't trust NIST. Such suspicion goes back to the 1970s when NIST, then called the National Bureau of Standards, proposed a weak cipher, the Data Encryption Standard that was easily broken by a brute force attack. NIST is working to improve the noise sources by adding some quantum-generated randomness. It's developed a workable quantum random number generator based on single photons of light using a technique called the Bell test.[17-19] The NIST quantum generator has been demonstrated to be a superior source of random numbers.[19] The NIST research team is able to extract 1,024 bits with uniformity of one trillionth of 1 percent from 55,110,210 trials of the Bell test.[19]
References:
- A Million Random Digits with 100,000 Normal Deviates, RAND Corporation, The Free Press (1955).
- George W. Brown, "History of RAND's random digits—Summary," in A.S. Householder, G.E. Forsythe, and H.H. Germond, eds., Monte Carlo Method, National Bureau of Standards Applied Mathematics Series, vol. 12 (Washington, D.C.: U.S. Government Printing Office, 1951), p. 31 ff.
- Jens Boos, "The Nixie Tube Story," IEEE Spectrum, July 25, 2018.
- Eshan Chattopadhyay and David Zuckerman, "Explicit Two-Source Extractors and Resilient Functions," The Electronic Colloquium on Computational Complexity, March 20, 2016.
- New Method of Producing Random Numbers Could Improve Cybersecurity, University of Texas Press Release, May 16, 2016.
- Landon Curt Noll, Robert G. Mende and Sanjeev Sisodiya, "Method for seeding a pseudo-random number generator with a cryptographic hash of a digitization of a chaotic system," US Patent No. 5,732,138, March 24, 1998.
- Christian Gabriel, Christoffer Wittmann, Denis Sych, Ruifang Dong, Wolfgang Mauerer, Ulrik L. Andersen, Christoph Marquardt and Gerd Leuchs, "A generator for unique quantum random numbers based on vacuum states," Nature Photonics, vol. 4 (August 29, 2010), pp. 711-715, doi:10.1038/nphoton.2010.197
- M. Matsumoto and T. Nishimura, "Mersenne Twister: A 623-Dimensionally Equidistributed Uniform Pseudo-Random Number Generator", ACM Transactions on Modeling and Computer Simulation, vol. 8, no. 1 (January, 1998), pp 3-30, doi:10.1145/272991.272995. A PDF copy can be found here,
- Takuji Nishimura, "A C-program for MT19937: Integer version," April 6, 1998.
- George Marsaglia, "64-bit KISS RNGs, The Coding Forums, February 28, 2009.
- Diehard Tests, Florida State University Statistics Website.
- Robert G. Brown, Dirk Eddelbuettel, and David Bauer, "Dieharder: A Random Number Test Suite, Version 3.31.1," Duke University Web Site.
- How Useful Is NIST's Randomness Beacon, Stack Exchange, March, 2014.
- NIST Randomness Beacon Summary.
- NIST Randomness Beacon Slide Presentation (PDF File).
- Home page of the NIST Randomness Beacon.
- Sophia Chen, "Why are countries creating public random number generators?" Science, June 28, 2018, doi:10.1126/science.aau6171.
- Peter Bierhorst, Emanuel Knill, Scott Glancy, Yanbao Zhang, Alan Mink, Stephen Jordan, Andrea Rommal, Yi-Kai Liu, Bradley Christensen, Sae Woo Nam, Martin J. Stevens, and Lynden K. Shalm, Experimentally generated randomness certified by the impossibility of superluminal signals, Nature, vol. 556, no. 7700 (April 1, 2018), pp. 223-226, https://doi.org/10.1038/s41586-018-0019-0.
- New quantum method generates really random numbers,National Institute of Standards and Technology Press Release, April 11, 2018.
- Casting Lots in the Digital Age, This Blog, June 23, 2016.
- Patterns from Randomness, This Blog, May 18, 2017.
- One Time Pads, This Blog, June 12, 2013.
- Random Coprimes and Pi, This Blog, October 10, 2016.