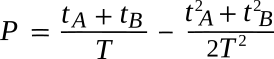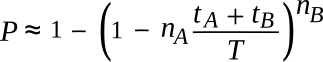Collisions

April 6, 2017

When a physics blog presents an article about collisions, one might assume that the topic is classical mechanics, or the statistical mechanics that leads to the thermodynamic behavior of gases. Billiards is a good example of collisions between objects, and there are demonstrations of things such as the conservation of momentum using billiard balls. What's more interesting is the idea that elastic collisions between billiard balls can be used for computation.

The idea of a billiard ball computer appears in a 1982 paper by Edward Fredkin and Tommaso Toffoli.[1] Fredkin is noted also for the concept of the Fredkin gate, a logic gate that allows reversible computing. The Fredkin gate is universal, meaning that any logical operation can be done using Fredkin gates. Fredkin was co-inventor, with Marvin Minsky, of the Triadex Muse music synthesizer, a device that produced algorithmic musical sequences based on parameter settings for pitch, volume, and tempo.[2]

Fredkin is also a proponent of the interesting concept that the laws of physics actually arise from a simple algorithm that controls the operation of the universe. The complexity of today's universe is explained by the idea that iteration of this simple algorithm has been going on for a long time. I'm reminded of John Wheeler's "It from bit" concept that I wrote about in a previous article (It from Bit, July 8, 2013).

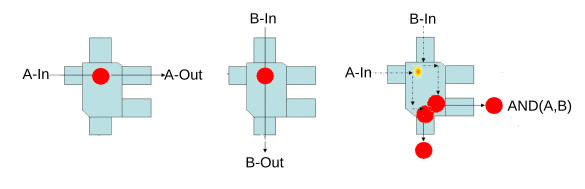
Fredkin and Toffoli's fundamental concept was that a computer could be built as a suitably-shaped container filled with an ideal gas, the elastic collisions of the ideal gas molecules, constrained to move within the passages of the container, doing the computation. In an upwardly scaled conceptual model, perfectly elastic billiard balls on a frictionless platform replace the ideal gas molecules. An example billiard ball logic gate is shown in the figure.

A billiard ball implementation of an AND gate, as proposed by Fredkin and Toffoli. When two balls simultaneously enter the gate, their collision results in the ejection of one ball through the output port. It can be seen that synchronization of the input signals is essential to proper operation. (Wikimedia Commons image, modified using Inkscape.)

Now that we've entered of realm of the "Internet of Things," there are many devices in our homes, offices, and factories that collect data for transmission to a central server. Since many of these devices are battery-powered, or rely on environmental energy-harvesting techniques for power, they transmit infrequently. As an energy-savings measure, they don't listen before transmission, and this leads to another type of collision when two devices transmit data at the same time.

The only way that a receiver can handle such a collision is to discard both data streams and obtain the data at a later time when there is no collision. If the transmitting devices are somehow synchronized, as when they are identical devices, started at the same time, and running the same code, their data will just collide at the next transmission time. One way to prevent collision is to have the devices transmit at random intervals; provided, however, that identical devices can be seeded to yield different random sequences.

If such devices do transmit at random intervals, how often would collisions occur? Fabian Schneider has published a paper on arXiv that provides some insight into this problem.[3] Schneider has provided equations for determining the probability P of two randomly occurring independent events, A and B, will occur simultaneously when they happen n_A and n_B times in an interval T and last for periods t_A and t_B. He gives the following example for the process.

"John works inside his office for 2 hours. A blue car will occur 10 times on the nearby street and remains visible for 1 minute each time. John looks outside 5 times for 3 minutes each. How likely is John going to see a blue car?: T = 120 min, t_A = 3 min, t_B = 1 min, n_A = 5, n_B = 10 and we are about to determine P (120, 3, 1, 5, 10)."[3]

Schneider presents an exact solution for the case in which the events, A and B, occur just once in the interval, as follows:

He also presents a close approximation of P for any given values of n_A and n_B.

I tested these results with a computer simulation (C language source code here). For the case of events, A and B, occurring just once in the interval, I got the following result.

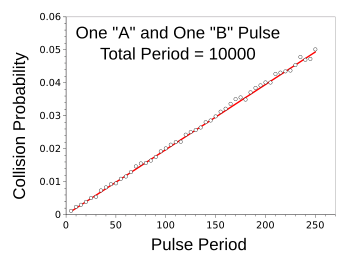Collision probability as a function of pulse width, for one A and one B pulse of the same width in an interval. The red line shows the predicted values. (Computer simulation data, graphed using Gnumeric.)

The fit of the equation to the data is superb. For the case in which the events, A and B, occur ten times in the interval, I got the following result.

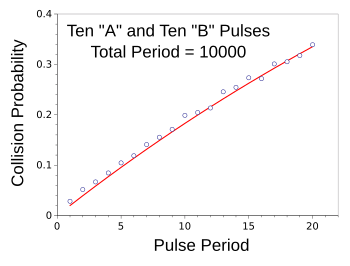Collision probability as a function of pulse width, for ten A pulses and ten B pulses of same width in an interval. The red line shows the predicted values. (Computer simulation data, graphed using Gnumeric.)

The fit of the data to the second, approximation, equation is also superb.

References:

1. E. Fredkin and T. Toffoli, International Journal of Theoretical Physics, vol. 21, no. 3 (April, 1982), pp. 219-253, doi:10.1007/BF01857727.
2. Edward Fredkin and Marvin L Minsky, "Digital music synthesizer," US Patent No. 3,610,801, October 5, 1971.
3. Fabian Schneider, "How likely are two independent recurrent events to occur simultaneously during a given time?" arXiv, December 23, 2016