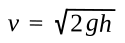Tikalon Blog by Dev Gualtieri

Torricelli's law

January 23, 2017

Vacuum chambers are a staple of nearly every solid state physics laboratory. I had several in my own laboratory for such purposes as physical vapor deposition, electron beam excitation of phosphors, and high voltage testing of electrical insulators. While those systems achieved vacuums in the range of 10^-9 atmospheres, my colleagues doing molecular beam epitaxy had systems that achieved a vacuum several orders of magnitude better than that.

What do such vacuum pressures mean when you're doing an experiment? There's a physical constant, called Loschmidt's number, that's the number of molecules in an ideal gas in a volume at standard temperature and pressure, 0°C (273.15 K) and 100 kPa (about one atmosphere). This is 2.687 x 10²⁵ per cubic meter. This constant is named after the Austrian physicist, Johann Josef Loschmidt (1821-1895), who gave the first estimate of the size of molecules.

Commemorative plaque at the house of Johann Josef Loschmidt (1821-1895)

Commemorative plaque at the house in which Loschmidt lived from 1890-1895.

Loschmidt is famous, also, for Loschmidt's paradox that the time-reversal symmetry of particle motion in classical mechanics is at odds with our observation that entropy is always increasing.

(Photo by Wolfgang Dvorak, via Wikimedia Commons.)

An ultra high vacuum system of the type suitable for molecular beam epitaxy, achieves a vacuum of about 10^-12 atmospheres. Calculation using Loschmidt's number shows that even at a vacuum of 10^-12 atmospheres there are still 2.687 x 10¹³ gas molecules per cubic meter in our vacuum chamber. Most vacuum chambers are just a tenth of this volume, so we're dealing with about 10¹² molecules. This still seems large, but a square centimeter of the surface of a typical (110) silicon wafer contains about 10¹⁵ atoms, and not every molecule in the atmosphere will contact the surface.

In my laboratory, my vacuum gauges didn't give the pressure in atmospheres. The typical laboratory unit of vacuum pressure is the torr, named after the Italian physicist, Evangelista Torricelli (1608-1647). Torricelli invented the mercury barometer, and his device also demonstrated why water can't be raised more than ten meters by a pump. That's because the pushing force on the water column is the differential pressure between the pump and the atmosphere, and it will attain a maximum at a perfect vacuum.

In analogy to water pumping, Torricelli's barometer could be used as a vacuum gauge in which the height of the mercury in a column showed the strength of the vacuum; thus, millimeters of mercury was a measure of vacuum, and this measure, now quantified as 101325/760 pascals ≈ 133.3 Pa, is known as a torr in his honor. The 760 comes from the typical height of mercury in a barometer exposed to the atmosphere, and the 101,325 is the number of pascals in an atmosphere.

Italian physicist, Evangelista Torricelli (1608-1647).

(Portrait at the Museo Galileo of Florence, via Wikimedia Commons.)

Torricelli, who apparently enjoyed explaining hydraulics using the physics of mechanics, is also famous for Torricelli's law that explains how fast fluid will flow out of a hole in its container. Most readers may have discovered the fact that fluid flows more quickly through a funnel if it's always topped-off, and this is quantified by Torricelli's law.

Torricelli found that the speed at which a fluid exits a hole in a container is a function of the height of the fluid above the hole, a simple consequence of gravity. According to this law, the exit speed v is given as

where g is the gravitational acceleration, about 9.8 m/sec² at Earth's surface, and h is the height of the fluid above the hole.

I've always enjoyed doing simple experiments at home, and it was fun advising my children when they were doing their school science fair projects. Seeing the popular cookbook, "The Joy of Cooking," in our kitchen made me think about publishing a "Joy of Experiment" book. Alas, I was preempted in 2011 by publication of the book, "The Joy of Physics," by Arthur W. 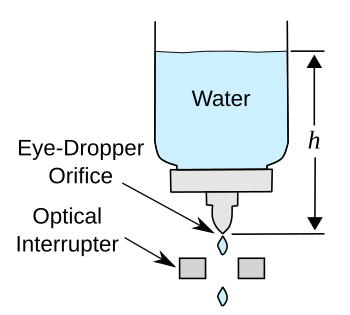Wiggins.[1] However, I was still inspired to verify Torricelli's Law using a computer for data acquisition. A schematic of the experiment appears below.

My experiment to test Torricelli's law.

The optical interrupter is connected to a computer to count droplets as they fall through the gap.

(Drawn using Inkscape.)

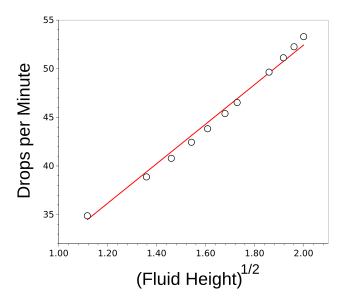
In this experiment, the drop rate is the equivalent of the flow rate, and the data analysis is straightforward. The container held about three cups of water (about 700 mL), the initial fluid level was four inches, and it was reduced to one inch over the course of the experiment. As can be seen by the results shown in the next two graphs, Torricelli's Law seems to be true over this small change in fluid height.

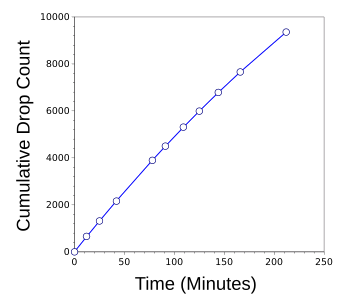Cumulative count rate of water drops as the fluid level decreased from four inches to one inch.

Although not visually apparent from this graph, the drop rate decreased considerably.

(Graphed using Gnumeric.)

Experimental data recast in terms of Torricelli's law by graphing the drop rate as a function of the square-root of fluid height.

The linear fit is what would be expected from Torricelli's Law.

(Graphed using Gnumeric.)

As can be deduced from its simplicity, the equation for Torricelli's Law is the solution for an idealized case. One ignored factor is the interaction between the fluid and the material of the container and the exit orifice. This interaction was addressed in a recent paper in Physical Review Letters by physicists at the École Normale Supérieur de Lyon (Lyon, France), who found that the hydrophilicity of the exit orifice affects the draining rate. [2-3] They've shown that the hydophilic property of the container's surface also plays a role, explaining why identically shaped tanks will empty at different rates.[3]

One surprising result of their experiments was that the exit speed goes through a minimum as the surface property of the bottom plate of the container changes from hydrophilic to hydrophobic.[2] Maximum slowing, about 20%, was achieved at a static wetting angle (contact angle) of about 60°. The experiments suggest that cause of this phenomenon is the meniscus that forms at the exit outlet.[2] The research team was able to develop a simple model to predict the drainage speed as a function of the static wetting angle.[2]

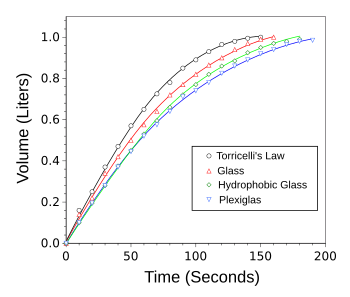Deviation from Torricelli's Law caused by the hydrophilicity of the container bottom plate.

The initial fluid volume was 1 liter, and the initial fluid height was 10 cm.

(Graphed using Gnumeric from data in ref. 2.[2])

The presence of the meniscus causes an accelerated draining rate compared to a completely straight jet.[3] The degree of acceleration depends on the shape of the meniscus, thus the importance of the hydrophilicity.[3]

Torricelli's law

References: