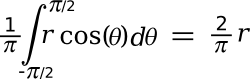The Drunken Jogger
January 4, 2016
I rarely watch
television, principally because most of the content isn't interesting to me; and, secondarily, because there are far too many
commercials. The later doesn't make much sense, since there's no requirement that you must have a certain number of commercials per hour, and having half as many commercials for which the
advertiser pays twice as much would give the same payout to the content owner.
Streaming content on the
Internet is now forcing
television networks to show fewer commercials in order to compete.[1]
Cable television is the
culprit in the increased frequency of television commercials. Before cable, television was available only through
broadcast stations licensed by the
Federal Communications Commission. According to the venerable
Communications Act of 1934, such stations were licensed just to use their
frequencies, they did not "own" their frequencies. They were considered to hold these frequencies "in
trust for the public," and were required to operate in the public interest.[2] Having too little content and too many commercials was not considered to be in the public interest.
One recent
evening, I was bored enough to give television a try. In scrolling through the
program guide, I found something interesting. It was an episode of
Drunk History, a strange program in which
drunken comedians recall an
historic American event while
actors lip sync to the
dialog. What piqued my interest was a topic of that particular show (
"New Jersey," Season 3, Episode 1, September 1, 2015).
That topic was the discovery of the
cosmic microwave background in 1964 by
Arno Penzias (b. 1933) and
Robert Wilson (b. 1936). The
narrator was
Jenny Slate, who did an excellent narration. Slate is an
alumna of
Milton Academy, the
alma mater of many notable people. Arno Penzias was played by
Justin Long, and Robert Wilson was played by
Jason Ritter. The
set design was very true to the period.
Seeing that episode starting my thinking about the
drunkard's walk, also known as a random walk. I wrote about random walks in an
earlier article (Random Walks and Lévy Flights, May 19, 2011). Before continuing, I should mention the 2008 best-seller,
The Drunkard's Walk: How Randomness Rules Our Lives, by American physicist,
Leonard Mlodinow (b. 1954);[3] and also,
Drunkard's Walk, a mathematics suspense novel by
Frederik Pohl (1919-2013), a notable
technical high school drop-out.
A drunkard's walk in
two dimensions generates a path that explores all directions in the
plane, and there's a variant, called a
self-avoiding random walk, in which the drunkard decides to never cross his own path. The drunkard's walk I decided to tackle was the constrained case of a drunken
jogger who always makes progress with each step along a
runway, although he veers from side to side with every step.
Since I haven't done a
computer simulation in a while, I decided to write a
C language program to simulate this drunken jogger's performance while jogging down a 5,000 step, 20 step wide, runway. This is a very easy program, executed in my usual amateur coding style, with
source code available
here. An example of the jogger's path can be seen in the graph, below.
 |
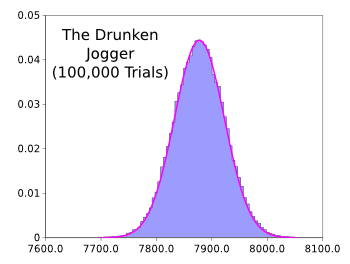
| Typical path of a drunken jogger in a track that's 20 steps wide. It takes the drunken jogger about 7885 steps to complete a 5000 step course.(Data graphed using Gnumeric.) |
If our jogger had run in a
straight line, his jog would have taken 5,000 steps. As the
histogram of his performance over 100,000 trials shows, he generally needs to take about 7885 steps to complete the course; that is, his path is about (7885/5000) = 1.577 times longer.
As they say, "
If the only thing you have is a hammer, everything looks like a nail." Being a
computer person, I had gone to a
keyboard, rather than a
notepad, to solve this problem. Embarrassed by that, I grabbed a notepad as an afterthought to see whether there was an
analytical solution. As it turns out, there is, and it was easier to do than writing the simulation. An explanatory diagram appears below.
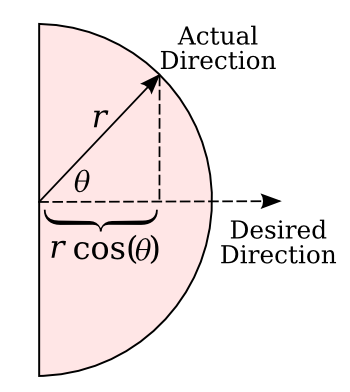 | Calculating the forward motion of the drunken jogger.
Taking a step of length r in a arbitrary forward direction θ results in a forward increment of r·cos(θ).
(Created by the author using Inkscape.) |
Our drunken jogger is motivated to always make forward progress (the Desired Direction), but he steps through
random angles θ that give a
component in the desired direction of just
cos(θ). We can calculate the average step size in the desired direction using a little
calculus, as follows:
The
coefficient,
2/π, has a value 0.63662, meaning that the average step in the forward direction is 0.63662 of a full step. As related to our jog down a 5,000 step runway, this means that the jogger needs to take (5000/0.63662) = 7854 steps, which is quite close to our simulated value. The small difference may be a consequence of our simulation requiring the jogger to stay on the narrow runway, while the analytical solution does not.
References:
- Stephanie Topacio Long, "TV networks plan to show fewer commercials, and we have streaming to thank," Digital Trends, November 12, 2015 .
- Heidi R. Young, "The Deregulation of Commercial Television," Fordham Urban Law Journal, vol. 12, no. 2 (1983).
- Leonard Mlodinow, "The Drunkard's Walk: How Randomness Rules Our Lives," Vintage, May 5, 2009, 252 pp. (ISBN-13: 978-0307275172, via Amazon).