Visualization in Science and Math

June 30, 2016

My thought processes fall into two modes. As a background process, I often churn abstract ideas in my brain for days, or weeks, at a time. However, when my thoughts are directed at more concrete ideas, I need to scratch things out with pencil and paper. In this, I'm following in the tradition of Leonardo da Vinci, who left voluminous notebooks filled with drawings. One example is his helicopter, also called his air screw, as shown in the figure.

Leonardo da Vinci's helicopter. Da Vinci, who was a keen observer of nature, may have gotten the idea for this "air screw" from the winged seeds of trees such as the maple. (Wikimedia Commons image.)

A 2011 article in Science by Shaaron Ainsworth of the University of Nottingham (Nottingham, UK), Vaughan Prain of La Trobe University (Bendigo, Australia), and Russell Tytler of Deakin University (Waurn Ponds, Australia), cites further examples in the notebooks of Michael Faraday and James Clerk Maxwell. Since scientists use visual representations to innovate and test new ideas, these authors propose that students of science would be more engaged if their courses had less of an emphasis on rote learning, instead having the students sketch scientific principles.[1]

Electronic engineers specializing in analog circuit design are always sketching circuit diagrams in notebooks, and often on tablecloths and napkins during luncheon meetings. Organic chemists are always sketching potential molecular configurations. Roald Hoffmann, who was awarded the 1981 Nobel Prize in Chemistry, has given many examples of molecular structures in his frequent articles in American Scientist.[2-3]

Nobel Chemistry laureate, Roald Hoffmann, holding a ball-and-stick model of a crystal. Such models have been guiding chemists since the discovery of the atomic nature of matter. One prominent example is the elucidation of the molecular structure of DNA by James Watson and Francis Crick. (Via Wikimedia Commons.)

While geometry, existing for more than two millennia, has always been a visual part of mathematics, it wasn't until the invention of the Cartesian coordinate system by René Descartes in 1637 that nearly every part of mathematics became visual. This Cartesian visualization assisted Isaac Newton and Gottfried Wilhelm Leibniz in their development of calculus in the 17th century (see figure).

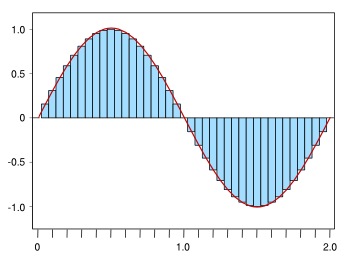Integral of the sine function, approximation by rectangles. The x-axis is in units of pi. The area under each half-sine wave is 2, but their sum is zero. (Created using Gnumeric.)

Computer graphics have aided scientific and mathematical visualization. As I wrote in an earlier article (Visualizing Science, November 9, 2010), a research team from Los Alamos National Laboratory used anonymized data from twenty three online database providers to see how scientists move between articles in different specialty journals. In this way, the Los Alamos team was able to capture 346,312,045 transactions to map the connections between scientific fields.[4] That's quite an advance over what I could do with graph paper and a pencil in my student days.

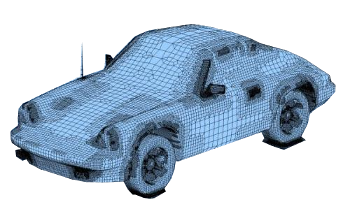Engineering has been assisted by computer aided design (CAD). This is a finite element model of a Porsche 911 automobile. (Modified Wikimedia Commons image.)

The periodic table of the elements is usually just a convenient reference chart, and it's an iconic wall hanging in most laboratories. While the typical format of the periodic table, as can be seen on Wikimedia Commons, has always served me well, scientists have constructed alternative visualizations to emphasize one property or another. Two interesting examples are shown below.

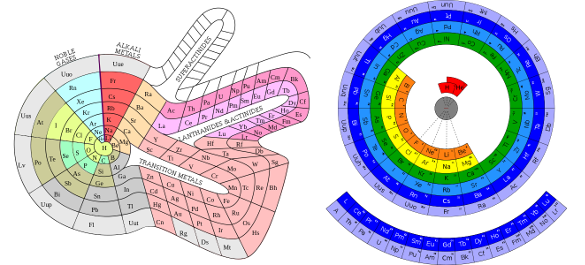Two spiral format periodic tables. (Click for larger versions of the left and right tables on the Wikimedia Commons Web Site. Left image by DePiep, and right image by Chris Buckley)

While the prime numbers could constitute a periodic table for mathematics, this would be a large table, indeed, since there are an infinity of primes. Although there are some periodicities in the prime numbers, as shown by the Ulam Spiral, these would be well hidden in a table containing a small subset of the primes. Now, a team of more than 80 mathematicians from 12 countries has developed a different sort of periodic table of mathematics, and they've launch a website, www.lmfdb.org, to contain this information.[5-6]

The LMFDB, more properly, the database of L-functions, modular forms, and related objects, was developed through thousands of hours of human effort and hundreds of CPU years.[5] More than 20 million objects are contained in the database, and each item has a link to related items.[5] Says John Voight, an associate professor of mathematics at Dartmouth College and a member of the LMFDB project team,

"Our project is akin to the first periodic table of the elements. We have found enough of the building blocks that we can see the overall structure and begin to glimpse the underlying relationships."

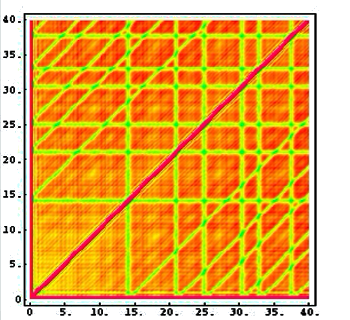A representation of the triple correlation of the zeros of the Riemann zeta function. The stripes arise from the influence of the first few zeros on the later zeros. (Image courtesy of Nina Snaith.)

The motivation for this work is to build connections between apparently unrelated areas of mathematics, as Descartes did when he merged algebra with geometry in his coordinate system. One modern example is how Andrew Wiles, in his proof of Fermat's Last Theorem, used a connection between elliptic curves and modular forms.[5]

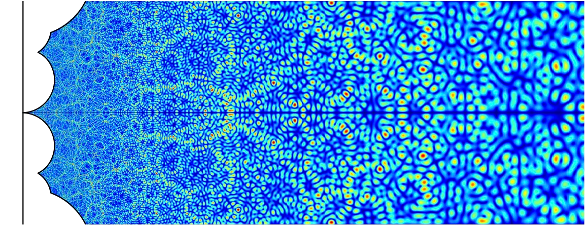A Maass form, one of the different types of objects in the database of L-functions, modular forms, and related objects.(Image by Fredrik Strömberg.)

Mathematicians are using computers more often for discovery, and the availability of cloud computing has led to an enhanced capability in this area. As an example, MIT's Andrew Sutherland used 72,000 cores of the Google Compute Engine to complete in hours a tabulation that would have required at least a century on a single computer.[5] More than 100 research papers reference the data in the LMFDB.[5]

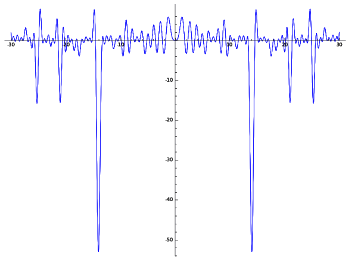An aural visualization can be done by mapping number values to audio frequencies. This waveform is the the Z-function of the first rank-4 elliptic curve, rendered in sound in this mp3 file. (Image courtesy of LMFDB.)

References:

1. Shaaron Ainsworth, Vaughan Prain, and Russell Tytler, "Drawing to Learn in Science, Science," vol. 333, no. 6046 (August 26, 2011), pp. 1096-1097. A PDF file of this article can be found here.
2. One example, from many, is Roald Hoffmann, "The Many Guises of Aromaticity," American Scientist, vol. 103, no. 1 (January-February 2015), pp. 18ff., DOI: 10.1511/2015.112.18.
3. Roald Hoffmann Web Site.
4. Johan Bollen, Herbert Van de Sompel, Aric Hagberg, Luis Bettencourt, Ryan Chute, Marko A. Rodriguez and Lyudmila Balakireva, "Clickstream Data Yields High-Resolution Maps of Science," PLoS ONE, vol. 4, no. 3 (March 11, 2009), article e4803, http://dx.doi.org/10.1371/journal.pone.0004803. The scientific field map can be found at this link.
5. Exploring the mathematical universe - Uncovering new worlds along the way, American Institute of Mathematics, May 10, 2016.
6. LMFDB, the database of L-functions, modular forms, and related objects.