Tikalon Blog by Dev Gualtieri

Mathematical Astronomy in Babylon

March 10, 2016

My science education started with children's science books. One of these was "The World of Science," and another was the "Golden Book of Science."[1] The full title of the latter book was, "The Golden Book of Science for Boys and Girls." The author of that book was a woman, Bertha Morris Parker, and this probably explains such an early excursion into gender equality in the sciences. The premier children's mathematics book of my generation was Irving Adler's, "The Giant Golden Book of Mathematics," Illustrated by Lowell Hess (Golden Press, New York, 1960).[2]

The Golden Book of Science for Boys and Girls by Bertha Morris Parker (1956).

This profusely illustrated book was an inspiration for many young scientists.

It's interesting how far science has advanced in the sixty years since publication of this book.

(Scan of the cover of my copy.)[1]

One frequent topic in children's books at that time was the Seven Wonders of the Ancient World, as listed below.

	Ancient Wonder	Date
	Great Pyramid of Giza	2584–2561 BC
	Hanging Gardens of Babylon	c. 600 BC
	Temple of Artemis at Ephesus	c. 550 BC
	Statue of Zeus at Olympia	466–456 BC
	Mausoleum at Halicarnassus	351 BC
	Colossus of Rhodes	292–280 BC
	Lighthouse of Alexandria	c. 280 BC

While the existence of the Giza Pyramid is quite evident, and the existence of all but one of the other "wonders" is verifiable, the location of the Hanging Gardens of Babylon has never been established. They were thought to have been built by King Nebuchadnezzar II in 600 BC in the ancient city of Babylon, located in today's Iraq. The Hanging Gardens might have been purely mythical, or they may have just described a known garden built by the Assyrian king, Sennacherib, in nearby Nineveh.

The Hanging Gardens of Babylon, as painted in 1886 by Ferdinand Knab (1834-1902) as part of his "Seven Wonders of the Ancient World" series.

(Via Wikimedia Commons.)

Although we question Babylonian excellence in gardening, there's no question that Babylonian mathematics was advanced for its time. One quirk of Babylonian mathematics was its number system, which was sexagesimal; that is, it was a base-60 system. This number system, probably inherited from the Sumerians, had some logic behind it. Sixty is a highly composite number, having as factors, 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, and 60. A Babylonian cook would have an easy time scaling recipes.

Some representative Babylonian numbers, illustrating how quantities were inscribed by a simple wedge-tipped stylus into clay tablets. fractional numbers, as given in modern notation, have the form a; b, c, d, which has the decimal equivalent a + (b/60) + (c/3600) + (d/60³), etc. (Modified Wikimedia Commons image by Josell7.)

This sexagesimal number system might be the reason why we have 360 degrees in a circle. The Babylonians used an inscribed hexagon to divide a circle, and each sixth of that circle was further divided by 60, resulting in 360 degrees.

Like most other ancient people, the Babylonians were avid astronomers, and they recorded their astronomical observations on clay tablets. As an example, the Venus tablet of Ammisaduqa, which dates to about 1650 BC, records the risings and setting times of Venus over a period of 21 years. There's even an observation of Halley's comet in 164 BC (see figure).

Perhaps it was practice in deciphering the hen-scratching of students that enabled the deciphering of this tablet.

A Babylonian tablet, now at the British Museum in London, recording the appearance of Halley's comet in 164 BC.

(Photograph by Linguica, via Wikimedia Commons.)

In a recent article in Science, Mathieu Ossendrijver of Humboldt University (Berlin, Germany), an astrophysicist who became an astroarchaeologist, writes that Babylonian mathematics, as applied to astronomy, had geometrical operations that anticipate modern calculus.[3-5] He discovered five clay tablets of the period 350-50 BC that explain the motion of the planet, Jupiter, using a trapezoidal construction of velocity data as a function of time.[3,5]

Jupiter was a prime object of study in Babylonian astronomy, since Jupiter was identified with their principal deity, Marduk (see figure). While pondering the significance of some clay tablets, Ossendrijver was gifted with photographs of a similar, uncataloged tablet at the British Museum by Assyriologist, Hermann Hunger of the University of Vienna.[4] Ossendrijver was able to connect the trapezoidal calculation of four tablets with Jupiter through this additional tablet.[5]

Babylonian god, Marduk, associated with the planet Jupiter

The Babylonian god, Marduk, as found on a cylindrical seal.

Marduk, who is associated with the planet, Jupiter, is shown on the seal with his pet dragon, sirrush.

Zeus, the principal deity of the ancient Greeks, and Jupiter, the principal deity of the Romans, were also identified with the planet Jupiter.

(Modified Wikimedia Commons image.)

As most of us remember, the trapezoidal method of finding the area under a curve was a prelude to integral calculus. In the Babylonian tablets, such a construction was used to interpolate the position of Jupiter through ratios of the areas under the velocity vs time curve. The area under such a curve, velocity multiplied by time, gives distance. In this astronomical case, the velocity is degrees per period, so the distance is specified as degrees (see figure). Such an operation was first seen in Europe in the 14th century.[3]

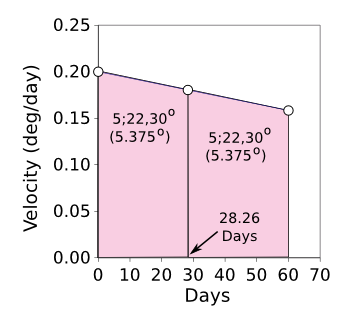Equal area construction for the motion of Jupiter.

The areas are given in sexagesimal notation and their decimal equivalent.

(Created from data in ref. 3 using Gnumeric and Inkscape.[3])

Mathematical Astronomy in Babylon

References: