Tikalon Blog by Dev Gualtieri

Tiling

September 24, 2015

Every technological age can be identified by its materials. For the Industrial Revolution, these were primarily iron and coal. The computer age is linked with silicon, but my childhood seemed to be the age of linoleum.

Linoleum, named for its principal ingredient, linseed oil, was invented in 1855, but its popularity as a floor tile peaked in the 1950s. The corridors of my elementary school were a sea of square linoleum tiles, chosen for that purpose because they were very easy to clean.

Complete coverage of a surface is called tiling. There are a multitude of ways to tile planar surfaces with geometrical shapes. Although the floor tiles of my school were square, nature seems to prefer hexagonal tiling, as shown in the figure. Humans have mimicked nature by using hexagons for tiling.

Left image, graphene; middle image, honeycomb; and right image, hexagonal pavement tiles by Claudine Rodriguez; all via Wikimedia Commons.

When you constrain yourself to regular tiling using just one type of regular polygon, you're limited to hexagons, as shown above figure, triangles, or squares. While you can place three regular hexagons, four squares, or six equilateral triangles around a vertex, you can't do that with a pentagon, or any polygon with more than six sides.

The pattern of blocks for my patio.

This is a very common tiling for rectangles whose length is twice the width, and it can be visualized as a shading of a square tiling.

(Photo by author)

As Johannes Kepler noted in his Harmonices Mundi, the 1619 work in which he published his third law of planetary motion, you can complete tiling with regular pentagons by adding three additional shapes (see figure).

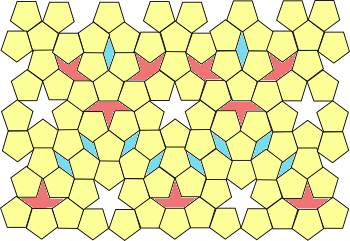Keplerian pentagonal tiling.

(Created with Inkscape.)

Once we allow our tilings to include more than one shape, a vast panoply of designs has opened. As an example, the figure below shows how two six-sided shapes can fill a plane with a more artistic effect than a simple hexagonal tiling.

Tiling hexagons with another six-sided figure.

(Illustration by Tadeusz E. Dorozinski, via Wikimedia Commons.)

The previous examples are tilings having translational symmetry; that is, the pattern is formed by just stacking a primitive object horizontally and vertically in the plane. Even the Keplerian tiling of pentagons and three other shapes has a group of elements that can be repeatedly stamped to fill the plane. However, there are aperiodic tilings without translational symmetry.

A Penrose tiling, named after mathematician, Roger Penrose, tiles the plane using an aperiodic set of prototiles. A Penrose tiling does not have translational symmetry, and it's an example of a two-dimensional quasicrystal with a diffraction pattern having five-fold rotational symmetry. An example of Penrose tiling appears below, and a nice summary of Penrose tiling and other tiling appears as ref. 2.[2]

A Penrose rhombus tiling with five-fold rotational symmetry.

Roger Penrose was issued a patent on his tiling in 1979.[3] This patent, which has now expired, gives directions for creating such tilings.

(Modified Wikimedia Common image).

Although regular pentagons will not by themselves tile a plane, relaxing the requirement to any convex polygon of five sides yields quite a few pentagonal tilings. Up to the present, fourteen had been found, and these are shown on their Wikipedia page. Just last month, three mathematicians from the University of Washington Bothell, Casey Mann, Jennifer McLoud, and David Von Derau, discovered a fifteenth with help from a computer algorithm.[4-6] This follows discovery of the fourteenth by thirty years.

The German mathematician, Karl Reinhardt, discovered the first five classes of pentagonal tilings in 1918.[6] R. B. Kershner found three more in 1968, Richard James found an additional one in 1975, and Marjorie Rice, an amateur mathematician, discovered four further types.[6] Rolf Stein found the fourteenth in 1985.[6] Casey Mann, part of the team that discovered the new pentagonal tile that covers the plane, is quoted on NPR as saying,

"We discovered the tile using using a computer to exhaustively search through a large but finite set of possibilities... We were of course very excited and a bit surprised to find the new type of pentagon."[6]

The 15th pentagonal tiling, published in August, 2015, by Casey Mann, Jennifer McLoud, and undergraduate researcher, David Von Derau, of the University of Washington Bothell.

(Modified Wikimedia Commons image by Ed Pegg, Jr.)

Mann likens this discovery with finding a new elementary particle, and it could have practical application in biochemistry and chemistry, where molecules are constrained by geometry to form in just certain shapes, and in structural design.[4] Von Derau was already a professional software developer when he arrived at the university to complete his undergraduate degree, and he was recruited by the two other authors, both professors, to assist in their tiling research.[4]

Von Derau coded an algorithm the others had developed, and he ran it on a cluster of computers. Eventually, the pentagonal tile shown in the figure popped out of the program.[5] This tile is characterized by the angles shown, and the following side dimensions:

a=c=e
b=2a
d = 2a/((√2)((√3)-1))

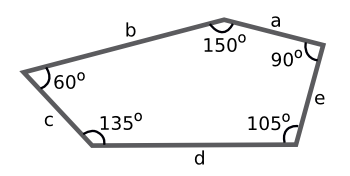The pentagonal tile used in the newly-discovered planar tiling.

(Wikimedia Commons image by Tom Ruen, modified using Inkscape.)

Von Derau's computer program is being ported to some high performance computers, and the search for additional tilings continues.[4]

Tiling

References: