Pi and the Quantum Realm

November 30, 2015

As Physics Nobel Laureate, Eugene Wigner, wrote in 1960,

"The miracle of the appropriateness of the language of mathematics for the formulation of the laws of physics is a wonderful gift which we neither understand nor deserve. We should be grateful for it and hope that it will remain valid in future research and that it will extend, for better or for worse, to our pleasure, even though perhaps also to our bafflement, to wide branches of learning."[1]

In this sentiment, Wigner was reframing in a modern context the 2,500 year old statements by the Greek philosopher, Pythagoras, that "Mathematics is the way to understand the universe," and "Number is the measure of all things."[2] Mathematics is a good friend of most scientists, who, as Ernest Rutherford said, would otherwise be doing "stamp collecting."[3] I wrote about science and mathematics in a previous article (Science and Math, July 16, 2012).

Pythagoras from the Nuremberg Chronicle, 1463. Woodcut attributed to Michel Wolgemut and Wilhelm Pleydenwurff (Via Wikimedia Commons).

As they say, "the proof of the pudding is in the eating." Galileo, the first modern physicist, used mathematics to successfully express the results of his experiments. As he wrote in The Assayer,

"Philosophy is written in this grand book — I mean the universe — which stands continually open to our gaze, but it cannot be understood unless one first learns to comprehend the language in which it is written. It is written in the language of mathematics, and its characters are triangles, circles, and other Geometric figures, without which it is humanly impossible to understand a single word of it; without these, one is wandering about in a dark labyrinth."[4]

One mysterious connection between mathematics and the quantum realm was discovered by Wigner, who found that random matrices closely describe the nuclear excitations of heavy atoms.[5] He found that the spacing between the energy levels of highly excited states of heavy nuclei resemble the spacings between the eigenvalues of a random matrix. It appears that God does play dice with the world.

A University of Rochester (Rochester, New York) physicist and mathematician were recently surprised to find the mathematical constant, pi, hidden in a quantum mechanical calculation for the energy states of the hydrogen atom.[6-8] Says mathematician, Tamar Friedmann, coauthor of a paper on this discovery in the journal, Mathematical Physics,

"We didn't just find pi... We found the classic seventeenth century Wallis formula for pi, making us the first to derive it from physics, in general, and quantum mechanics, in particular."[7]

The Wallis formula is quite unlike the most important formulas for calculating pi. Those formulas are rapidly convergent series expansions, the most notable being one developed by the brothers, David Chudnovsky and Gregory Chudnovsky, that delivers three digits of pi per calculated term,

The Chudnovsky algorithm is a variation of one discovered by the mathematics prodigy, Srinivasa Ramanujan.

In contrast, the Wallis formula, as discovered by John Wallis (1616-1703), an English mathematician credited for introducing ∞ as the symbol for infinity, is a product formula, as shown.

Wallis' formula appeared in his 1656 book, Arithmetica Infinitorum, as shown below,

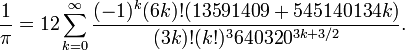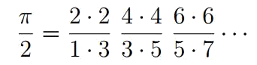A portion of page 179 from "Arithmetica Infinitorum" by John Wallis. Wallis, as did all scholars of his time, wrote in Latin. The product formula appears as its inverse. (Via Google Books.)

The Wallis formula appeared in calculations of the electron energy levels in the hydrogen atom. It was noticed while comparing the energy levels calculated using the variational approach with more accurate quantum calculations. The variational approach, which is simple enough to have been taught in the introductory quantum mechanics course I took in my graduate school days, is the quantum mechanical application of the variational principle that dates back to the least time principle of mathematician, Pierre de Fermat.[7]

While the variational approach is usually applied to calculations of electron energies close to the ground state, where it gives good values, the Rochester team applied it to excited states far from the ground state.[7] As physicist and coauthor, Carl Hagen, explains, "At the lower energy orbits, the path of the electron is fuzzy and spread out... At more excited states, the orbits become more sharply defined and the uncertainty in the radius decreases."[8]

Friedmann and Hagen compared the variational values to the known values by taking their ratios as a function of energy.[8] Examining the ratios, they saw that they yielded the Wallis formula for π.[7] The error in their variational approach calculation was about 15% for the ground state, 10% for the first excited state, and successively smaller at high energy levels. This was contrary to a typical variational calculation for which the better values are at the lowest energy levels.[8] The following is the product formula from their calculation.[8]

Says Hagen, "What surprised me is that the formula occurred in such a natural way in the calculations, with no circles involved in determining the energy states."[7] Mathematician, Friedmann, is impressed by this intimate connection of math and physics.

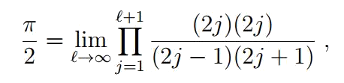"The special thing is that it brings out a beautiful connection between physics and math. I find it fascinating that a purely mathematical formula from the 17th century characterizes a physical system that was discovered 300 years later."[8]

The quantum behavior of electrons in hydrogen has been known for a century, but its connection to pi has been unknown for all that time. This discovery was notable enough that Friedmann and Hagen's paper was accepted in Mathematical Physics in less than 24 hours.[7]

References:

1. E.P. Wigner, "The unreasonable effectiveness of mathematics in the natural sciences," Communications on Pure and Applied Mathematics, vol. 13, no. 1 (February, 1960). pp. 1-14. A PDF file is available, here.
2. R. W. Hamming, "The Unreasonable Effectiveness of Mathematics," The American Mathematical Monthly, vol. 87, no. 2 (February, 1980), via the Center for Cancer Research Nanobiology Program.
3. Ernest Rutherford quotation page on Wikiquotes.
4. Selections of a translation of The Assayer; Stillman Drake, "Discoveries and Opinions of Galileo," Doubleday & Co.(New York, 1957), pp. 231-280.
5. E. Wigner, "Characteristic vectors of bordered matrices with infinite dimensions," Annals of Mathematics, vol. 62, no. 3 (November, 1955), pp. 548-564, doi:10.2307/1970079.
6. Tamar Friedmann and C. R. Hagen, "Quantum mechanical derivation of the Wallis formula for π," J. Math. Phys., vol. 56 (In Press, 2015), Document No. 112101, doi:10.1063/1.4930800. This is an open access paper with a PDF file available at the same URL.
7. Discovery of classic pi formula a ‘cunning piece of magic’, University of Rochester Press Release, November 10, 2015.
8. New derivation of pi links quantum physics and pure math, American Institute of Physics Press Release, November 10, 2015.
9. Derivation of the Wallis formula for pi on Wikipedia.