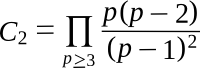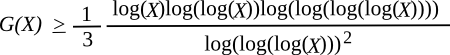Prime Gap

January 15, 2015

Before true knowledge of numbers, the first mathematics concept understood by children is likely the concept that one set of items is larger than another. Mothers realize this when they distribute candy pieces to their children. Arithmetic then dominates a child's mathematics education for the first few years of primary school. After that, he, or she, moves on to other things, such as trigonometry, geometry, and algebra, not realizing that there's an entire field of mathematics called number theory.

Prime numbers have an important place in number theory. A prime number is any natural number greater than one with no positive divisors aside from itself and one. All natural numbers are either prime, or composites; that is, numbers constructed by multiplying prime numbers together. The fundamental theorem of arithmetic asserts that any natural number greater than one can be expressed as a product of primes in just one way; thus, the famous taxicab number, 1729, is just 7 x 13 x 19, and it can't be expressed by any other combination of primes.

Eratosthenes at work. The Sieve of Eratosthenes is an algorithm for separating all prime numbers from the natural numbers. (Engraving after a work by the French painter Gustave Courtois (1853-1923), via arXiv.)[1]

Prime numbers become rare as we go to larger numbers, a property that's been quantified by the prime number theorem. This theorem states that the probability that a number N is prime will closely follow the function 1/log(N), where log() is the natural logarithm.

Twin primes are prime numbers that differ from each other by the smallest possible interval; namely, two. The first two twin prime pairs are (3,5) and (5,7), and there are 808,675,888,577,436 twin prime pairs below 10¹⁸. The list of twin primes is an integer sequence, designated OEIS sequence A077800. I wrote about twin primes in a previous article (The Twin Prime Conjecture, June 3, 2013)

Since prime numbers are less common as numbers get larger, twin primes become likewise rare. The twin prime conjecture, yet to be proved as a theorem, is that there's an infinite number of twin primes. This conjecture supposedly originated with the famous Greek geometer, Euclid, which would make it one of the oldest conjectures in number theory.[2]

Are there an infinite number of twin primes? As I wrote in a previous article (The Twin Prime Conjecture, June 3, 2013), Zhang Yitang, of the University of New Hampshire (Durham) advanced such a theorem by finding that there are infinitely many primes which differ in distance by at most 70 million.[6-7] Seventy million, of course, is quite a ways from two, but Zhang's result allowed others to reduce this limit to 246, so we've gotten really close, really fast.[8]

There are two constants associated with the twin primes. The first is the twin prime constant (C₂), 0.66016 18158 46869... (OEIS sequence A005597), defined as the following product of primes p:

The other is Brun's constant (B₄), the sum of the reciprocals of the twin primes, with the approximate value 0.87058 83800.

The spacing, or "gap," between twin primes is two, but the gap between consecutive primes takes on various values as we travel through the primes. Naturally, we find small gaps for smaller primes, and larger gaps for larger primes. These gaps are designated OEIS sequence A001223. If we confine our interest to the largest gap found, we see the trend in the following figure.

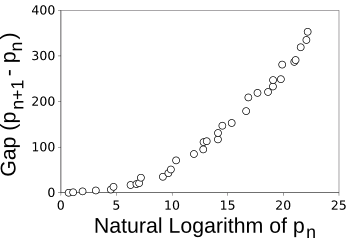The largest gap between prime numbers as a function of the first prime defining the gap. (Graphed by the author using Gnumeric.)

The graph above shows the longest gaps for numbers up to the limit of a 32-bit unsigned long integer in programming languages. If you're interested in getting more values, a 64-bit unsigned long long integer will raise the limit to 18,446,744,073,709,551,615, but your program might take a while to complete. I'm fairly certain that it would complete, the Entscheidungsproblem notwithstanding.

Such regularity makes us think that there's a function lurking, undiscovered, that would give the anticipated maximum gap for any number. The Scottish mathematician, Robert Alexander Rankin, produced the following result that expresses a minimum value for the gap G(X), for large numbers, as follows:[8]

The complexity of this formula notwithstanding, the behavior is close to a straight line on a semilog plot, as can be seen in the graph, below.

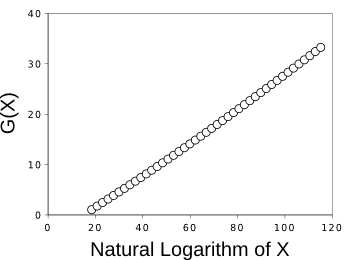Lower bound of the prime gap, as predicted by the Rankin formula. (Graphed by the author using Gnumeric.)

Although Rankin's formula is valid for the smaller primes, many mathematicians think that the gaps for larger primes must be greater, more on the order (log(X))². Gaps of this size would happen if the prime numbers acted as a collection of random numbers would, and primes have many properties in common with random numbers.[8]

The mathematician, Paul Erdos, had a conjecture that the appropriate formula would just be Rankin's formula in which the leading fraction of (1/3) was replaced by a function of X. As a consequence, the gap would be larger than Rankin's, but smaller than (log(X))².[8] Erdos, who died in 1996, established a prize for proof of his conjecture, and mathematician, Ronald Graham, a Bell Labs alumnus, now at the University of California, San Diego, has offered to honor the $10,000 prize.[8]

Ronald Graham and his wife, Fan Chung Graham, with Paul Erdos (left) in Japan, 1986. (Photo by Che Graham, via Wikimedia Commons.)

It appears that this conjecture has finally been proven. Terence Tao of the University of California, Los Angeles, Kevin Ford of the University of Illinois, Urbana-Champaign, Ben Green of the Oxford University, and Sergei Konyagin of the Steklov Institute of Mathematics, Moscow, have published a proof, and an independent proof has been published by James Maynard of Magdalen College, Oxford University.[9]

How would a mathematician tackle such a problem? The secret is in a way to construct long series of composite numbers using factorials, numbers that are symbolized by an exclamation point (!). As an example, 101!, the product of all natural numbers up to and including 101, is a composite number, since it's divisible by any of those numbers. Likewise, so are 101!+2 (divisible by two), 101!+3 (divisible by three), 101!+4 (divisible by four), etc.[8]

Mathematics is often not "useful," although the unexpected utility of some math is often found centuries after its discovery. This result may be found to be quickly useful, since prime numbers are used in cryptography. As Maynard points out, when you need a prime number for your algorithm, you might be unlucky enough to start testing for primes at the beginning of a huge gap.[8]

Tao is considering creating a new prize for a considered improvement of this result. As to the strange form of formulae such as Rankin's, Tao recalls a joke told among number theorists:

What does a drowning number theorist say?
"Log log log log … "[8]

References:

1. Khristo N. Boyadzhiev, "Eratosthenes and Pliny, Greek geometry and Roman follies," arXiv, June 15, 2010.
2. Maggie McKee, "First proof that infinitely many prime numbers come in pairs," Nature News, May 14, 2013.
3. Top Twenty Prime Gaps.
4. Chris K. Caldwell, "The Gaps Between Primes," The Prime Pages.
5. Chris K. Caldwell, "Table of Known Maximal Gaps," The Prime Pages.
6. Maggie McKee, "First proof that infinitely many prime numbers come in pairs," Nature News, May 14, 2013.
7. Erica Klarreich, "Unheralded Mathematician Bridges the Prime Gap," Simons Foundation Press Release, May 19, 2013. Same article on Wired.
8. Erica Klarreich, "Prime Gap Grows After Decades-Long Lull," Quanta Magazine, December 10, 2014. This article was reprinted on Wired.com.
9. Prime-gaps on Terry Tao's Blog.