Close Observation of Brownian Motion

April 28, 2014

Science often proceeds from accidental observations, and such an observation occurred in 1827 when Robert Brown, a botanist, was observing pollen grains under a microscopic. His sample contained not just pollen, but also amyloplasts, small, subsidiary particles associated with pollen grains, and spherosomes. Brown noticed that these were in a continual motion.

To exclude the idea that these motions arose from the biological nature of the particles, Brown found that this motion also existed in inorganic particles. This random motion of particles in fluids is now known as Brownian motion. It's caused by the impact of fluid molecules. Brownian motion is still an active research topic after all these years. ArXiv had 190 articles containing "Brownian" in their title in the years 2010-2013.

Scottish botanist, Robert Brown (1773-1858). Brown, who also did research in paleobotany, was among the first to use a microscope in his studies. These included the differentiation of gymnosperms from angiosperms (flowering plants). (Oil portrait by Henry William Pickersgill (1782-1875), via Wikimedia Commons.)

As I wrote in a previous article (Maxwell, Boltzmann and Brown, September 14, 2011), physicists from the Center for Nonlinear Dynamics and Department of Physics of the University of Texas at Austin (Austin, Texas) investigated the Brownian motion of individual micrometer-sized particles of silica glass beads in air.[1-2] The particles were held in place by an optical tweezer.

In those experiments, the temporal resolution of the measurement was fine enough to to observe the individual "hits" by the gas molecules, the so-called ballistic regime.[1-2]

In further work with colleagues at the Ecole Polytechnique Fédérale de Lausanne, the Texas team extended their observations to Brownian motion in a liquid with measurement of the motion of a particle to sub-Angstrom spatial resolution. The spatial resolution of these measurements was 20 picometers, which is about the size of a hydrogen atom, and the temporal resolution was about 15 nanoseconds.[3]

Motions of Brownian particles will ideally obey the Stokes-Einstein relation,

in which D, the diffusion constant, is related to the Boltzmann constant, k_B, the absolute temperature, T, the viscosity, η, and the particle radius, r. Plugging in the numbers shows that a one micrometer silica bead in water will move a nanometer every microsecond.

The Texas team has been improving their technique with results published in a recent issue of Science.[4] Their apparatus, as shown in the figure, consists of counterpropagating laser beams, one at 532 nm, and the other at 1064 nm. These are medium power lasers of about 200 milliwatts, but they're focused by water-immersion microscope objectives so that the power density incident at the liquid-suspended particles is large.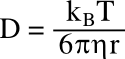

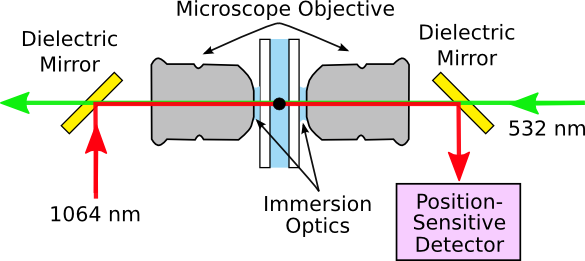Simplified diagram of the University of Texas at Austin optical tweezer apparatus for measurement of a particle's Brownian motion in a fluid. (Illustration by the author using Inkscape.)

Particles are introduced into the tweezer area by a flow-cell, and the horizontal motion of the optically-trapped particle is measured by a position-sensitive detector. A simplified diagram of the detector is shown in the figure. The detector signals are digitized and stored on a computer for later analysis.

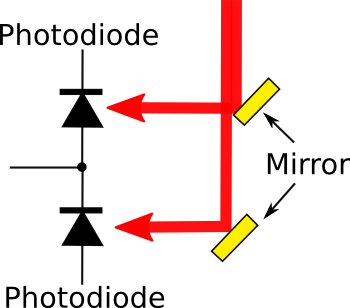It's all done with mirrors. The essential elements of the position sensitive detector used in the Texas experiments are two mirrors and two photodiodes. (Illustration by the author using Inkscape.)

The motivation of this research is explication of hydrodynamic effects that occur at very short time scales. The present apparatus is able to achieve shot-noise-limited position sensitivity below three femtometers per square-root-hertz in a bandwidth of 50 MHz. Two types of particles were used in the recent experiments, lighter silica, and heavier barium titanate glass. Fluids were water (1.00 cP at 20°C) and the less viscous acetone (0.33 cP at 20°C).

Analysis of two million velocity readings showed that the particle velocity agreed with the Maxwell-Boltzmann distribution within the experimental uncertainty. The root-mean-squared velocity of the barium titanate particles in acetone was 0.180 mm/s at 291 K. One indicator of interesting hydrodynamics was a small correlation between the particle velocity and thermal forces experienced at a future time. Causality, however, is intact, since the future forces are correlated with past forces.

As are so many things in Texas, this research was funded by the Sid W. Richardson Foundation and the Robert A. Welch Foundation.

References:

1. Tongcang Li, Simon Kheifets, David Medellin and Mark G. Raizen, "Measurement of the Instantaneous Velocity of a Brownian Particle," Science, vol. 328 no. 5986 (June 25, 2010), pp. 1673-1675.
2. Peter N. Pusey, "Brownian Motion Goes Ballistic," Science, vol. 332 no. 6031 (May 13, 2011), pp. 802-803.
3. Rongxin Huang, Isaac Chavez, Katja M. Taute, Branimir Lukić, Sylvia Jeney, Mark G. Raizen and Ernst-Ludwig Florin, "Direct observation of the full transition from ballistic to diffusive Brownian motion in a liquid," Nature Physics, vol. 7, no. 7 (July, 2011), pp. 576-580.
4. Simon Kheifets, Akarsh Simha, Kevin Melin, Tongcang Li, and Mark G. Raizen, "Observation of Brownian Motion in Liquids at Short Times: Instantaneous Velocity and Memory Loss," Science, vol. 343, no. 6178 (March 28, 2014), pp. 1493-1496.
5. Web Site of the Raizen Group at the University of Texas at Austin.