Tikalon Blog by Dev Gualtieri

Flower Power

January 29, 2014

The 1950s may have had their beatniks , but the 1960s were known for their hippies and flower children . Many members of my generation , as we attained college age, were understandably distressed by the state of the world at the time. Our general distrust of politicians fueled a counterculture movement in which many decided to "drop out" and not participate in any of the current social conventions .

Economists have always had their "guns or butter " debate, but in the 1960s it was "guns or flowers," sloganized by the term, "flower power ." Flowers were a symbol for peace ; but they have been symbols for many things, as their use for such disparate events as weddings and funerals shows.

An Iconic Image

Volkswagen buses were popular among hippies, since they were inexpensive, and you could live inside your vehicle.

(Photograph by Marshall Astor , via Wikimedia Commons .)

As I wrote in a previous article (Flowers, November 1, 2013), flowering plants (angiosperms) appeared at least as early as the Middle Triassic period, about 247.2-242.0 million years ago .[1-2] Flowers exist as a way to attract insects as an aid to pollination .

Because of evolution , nature seems to find the best way to do certain things. Humans have evolved to understand this, so we've developed the science of biomimetics , by which we research the structure and function of biological systems to aid in the design of materials and devices .

Computer scientists have embraced biomimetics in swarm intelligence . I wrote about one method of swarm intelligence, Ant Colony Optimization , in two previous articles (Computational Biomimetics, January 17, 2011 , and Ants in My Computer, November 8, 2006 ).

Ant Colony Optimization uses an analog of the technique that ants use to find the most direct pathway from a food source to their colony . This involves individual ants laying down a scent (pheromone ) trail that other ants roughly follow. Since the scent evaporates , the shortest path retains the strongest scent since more ants march over it per unit time interval. This technique has been used to place conductor traces on printed circuit boards , solving the traveling salesman problem, and routing messages in a network .[3-4]

At this point, you might be thinking that there's no logical thread in this article. Sure, you might expect to find ants on flowers, but that's about it. However, Xin-She Yang of Cambridge University has found that flower pollination can be used as the basis for a global optimization algorithm .[5] Yang has published previously on other biomimetic optimization algorithms, such as the firefly algorithm [6-7] and the bat algorithm [8-9].

Pollination is an important aspect of the survival of plant species , so it's understandable that an optimization algorithm based on pollination might be useful. As stated in Yang's paper on this topic, 80% of all plant species, about a quarter of a million, are flowering plants.[5] In a "selfish gene " perspective, the primary purpose of a flower is to reproduce by pollination, and in this task it's assisted by natural agents.

Pollination is aided by abiotic forces, such as water and the wind , and biotic agents, such as insects , birds , bats and other animals . Biotic pollination accounts for 90% of pollination.[5] There are at least 200,000 types of pollinators, the honeybee being the traditional example. Pollination can occur over short distances, as for self-pollination ; or, over long distances, in which the biotic pollinators may travel by a Lévy flight . I wrote about Lévy flight in a previous article (Random Walks and Lévy Flights, May 19, 2011).

Yang's flower pollination algorithm is quite simple, and it incorporates both local and distance pollination, as its function shows.[5]

• Initialize a population of gametes with random solutions.
• Find the best solution in the initial population
• Define a switch probability .
• Over the entire population, if a random number exceeds the switch probability, draw a vector obeying a Lévy distribution to "pollinate" another member of the population. This is "distance pollination."
• Otherwise, do a "local pollination" according to a normal distribution (a.k.a., Rayleigh flight).
• Evaluate the new population find the current best solution and repeat.

As they say, the proof of the pudding is in the eating , and the following figure demonstrates the potential of the flower pollination algorithm. Plotted is the difference D between the current solution and the best mean solution for a genetic algorithm (GA), a particle swarm optimization algorithm (PSO), and the flower pollination algorithm (FPA).

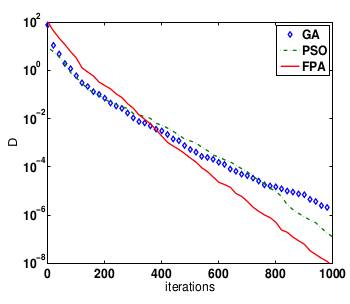Performance comparison between a genetic algorithm (GA), a particle swarm optimization algorithm (PSO), and the flower pollination algorithm (FPA).
The FPA has the best result, and it converged most quickly.

(Fig. 2 of ref. 3, via arXiv .[5])

Flower Power

References: