Tikalon Blog by Dev Gualtieri

Particle Clumping

July 9, 2014

Since our earliest days, each of us has been concerned with the common human activities of packing and filling. As children, we needed to pack our toys in our toy chest and our clothes in our dresser drawers and closet. We needed to fill our bowl with breakfast cereal without its overflowing, and the same for cups of milk. Not surprisingly, there's a lot of science behind the optimal packing and filling of regularly- and irregularly-shaped items.

As I wrote in a previous article (Packing and Filling, May 17, 2012) the optimal packing of circle in a plane occurs when their centers are on an hexagonal lattice . This packing gives an areal density of (π/2√3) = 0.9069 (see figure). Carl Friedrich Gauss proved that this packing was optimum for a lattice arrangement, and László Fejes Tóth showed that this is the optimal packing, lattice or otherwise.[1]

Lattice packing of pennies in a plane.

(Base image of a US penny, via Wikimedia Commons.)

Circles, of course, are an easy target, so it's more interesting to extend packing to other shapes in two dimensions, and to shapes in three dimensions, trying to determine what their maximum areal density and volume density might be. Computers are a big help in finding interesting phenomena, as the following figure demonstrates. This random packing of isosceles triangles was done using a variant of the Lubachevsky-Stillinger algorithm.

Random packing of isosceles triangles in a plane using a variant of the Lubachevsky-Stillinger algorithm.

(Illustration by L. Salgo, via Wikimedia Commons.)

In this example, as in many computer mapping on the plane, the boundaries were wrapped; that is, triangles stepping over the right edge stepped into the left edge. The same was true for the top and bottom edges. The areal packing density of the triangles in the figure is 0.8776.

As I discussed in an earlier article (Packing, November 30, 2010), jumping up one dimension to go from packing circles in a plane to spheres in a volume makes the mathematics much more difficult. The one obvious candidate for the densest packing of identical spheres is the cannonball stacking used also by greengrocers when they stack fruit. This close-packing arrangement is shown in the figure.

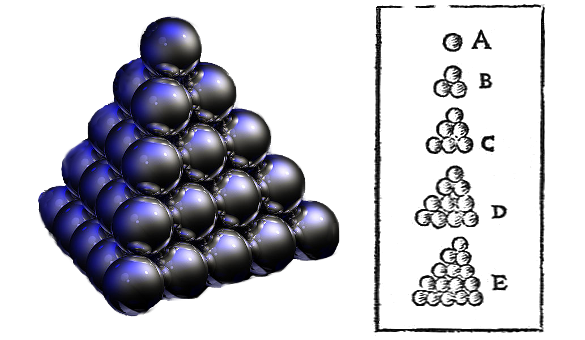The well-known cannonball (close-packing) arrangement of spheres (right), along with the illustration that Johannes Kepler (1571-1630) used when making the conjecture that this is the densest possible arrangement. (Left image by "Greg L," and right image from Johannes Kepler's 1611 Strena Seu de Nive Sexangula, both images via Wikimedia Commons.)

Johannes Kepler (1571-1630) conjectured that this arrangement of spheres, whose volume density is π/(3√2) ≈ 0.74048, has the highest possible density, and this was proved for lattice arrangements by Carl Friedrich Gauss (1777-1855). Note that stacking cannonballs on an equilateral triangle base and a square base gives the same packing, just with a different spatial orientation.

Proving that this packing was the densest packing for all sphere arrangements, lattice or otherwise, was not accomplished for quite some time. Finally, in 1998, Thomas Hales produced a "proof" which is much like the "proof" for the four color conjecture . He used computer programs to examine every possible case of sphere packing.[2]

If we're randomly packing spheres, the packing density comes in at 64%, which is quite a bit less than the 74% for close-packed lattice packing. In 2004, Princeton University physicist, Paul Chaikin (now at New York University), and chemist, Salvatore Torquato , found that random packing of oblate spheroids can be larger. M&M candy , for example, will randomly pack at 68%, while their lattice packing is about the same.[3-4]

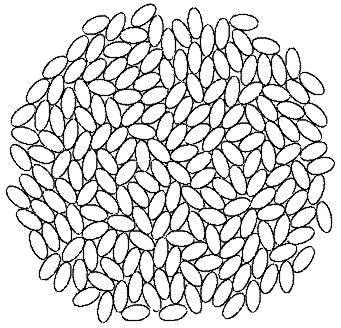Monte Carlo simulation of packing of hard ellipses.

(image from the ChaikinLab Condensed Matter Physics Laboratory at New York University.)

Their computer simulations found that a random stacking of ellipsoids, which are closer in shape to a sphere than the lenticular M&Ms, actually has a larger density than the close-packed lattice packing of spheres. Further work by Torquato [5-12] showed that the densest packings of tetrahedra , icosahedra , dodecahedra , and octahedra were 0.823, 0.836, 0.904, and 0.947, respectively. This is an interesting result, since the dodecahedra and icosahedra approximate a sphere to a high degree but pack much better.

Physicists use "spherical cow" models whenever possible, and it's easy to convince yourself that natural particles will aggregate in a manner similar to the packings described above. One important such aggregate, since it's implicated in global warming, is atmospheric soot, which is composed of round particles of carbon in a size range of about 10-20 nanometers. Scientists from the National Institute of Standards and Technology (NIST, Gaithersburg, Maryland) and the University of Maryland (College Park, Maryland) have measured the volume density of such weakly compacted aggregated materials, and they've found that it has a scale invariant value of about 0.36 over many orders of magnitude.[13-15]

Particle aggregates aren't limited to just atmospheric soot. They exist in interstellar dust clouds from which planets and comets are formed, and in microscale powdered pharmaceuticals.[13] Small aggregates grow into larger ones through compaction at low compression, so the size of aggregates covers ten orders of magnitude, from soot to comets.[13] What the research team has found is that the packing of aggregates is remarkably independent of the aggregating forces, the aggregation mechanism, and the initial conditions.[13]

After making measurements on soot particles, getting the volume density of 0.36, and convincing themselves that this was the correct value (they obtained 0.36 ± 0.02), the team decided to do some confirmatory experiments. They enlisted the help of a high school and a college intern (see photo), who glued thousands of random combinations of spheres in clumps of 1-12 spheres, filled various sized containers with these assemblies, and measured their volume fraction.[13]

Jessica Young, and intern at NIST, doing a packing experiment

Jessica Young, a high school student and an intern at NIST, doing a packing experiment.

Young's work aided NIST research on how rigid aggregates tend to clump together at roughly the same density regardless of scale.

(Image: Baum/NIST.)

The experiments proved that their hypothesis, that 0.36 is the most likely value for the packing density of an aggregate, was correct. This value obtains also for fine, compacted silica, as used in the manufacture of ceramics, and for pharmaceutical powders made from "microscale random aggregates." Measurements by NASA show that comet density is in the range of 0.2-0.4.[15]

Particle Clumping

References: