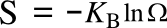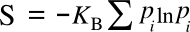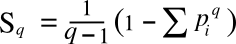Tsallis Entropy

October 29, 2014

Thermodynamics has developed from contributions from scientists of many nationalities. As just a few examples, we have Sadi Carno (1796-1832) from France; Robert Boyle (1627-1691) and William Thomson, Lord Kelvin (1824-1907) from Ireland; James Prescott Joule (1818-1889) from England; Rudolf Clausius (1822-1888) from Germany; James Clerk Maxwell (1831-1879) from Scotland; Josiah Willard Gibbs (1839-1903) from the United States; and Ludwig Boltzmann (1844-1906) from Austria).

Some founders of thermodynamics. Clockwise from the upper left, Carno, Boyle, Kelvin, Joule, Boltzmann, Gibbs, Maxwell, and Clausius. Images, via Wikimedia Commons, Carnot, Boyle, Kelvin, Joule, Clausius, Maxwell, Gibbs, Boltzmann. (Click for larger image).

It's only fitting that Greece, the origin of the Western intellectual tradition of philosophy and science, should also have been the birthplace of some prominent thermodynamicists. One of these is Constantin Carathéodory (1873-1950), whose profession was primarily mathematics.

In 1909, Carathéodory ventured into applied mathematics by working to formulate thermodynamics axiomatically. His book, "Investigations on the Foundations of Thermodynamics," sought to derive thermodynamics from mechanics. The importance of this approach is that he was able address irreversibility. Classical thermodynamics is accurately applied only to reversible processes, although bending of this rule still leads to acceptable results.

Constantin Carathéodory shown in military dress in his youth. This is apparently from his time at the Royal Military Academy in Belgium. Carathéodory's doctoral advisor was Hermann Minkowski, known for his work on special relativity. (Via Wikimedia Commons.)

Carathéodory's work is somewhat inaccessible because of all the mathematics, but another Greek thermodynamicist developed a modification of the classical Boltzmann entropy that's easy to understand. Constantino Tsallis (b. 1943) is a physicist who's a naturalized citizen of Brazil, but he was born in Athens, Greece, lived in Argentina, and he was awarded his doctotal degree in physics from the University of Paris-Orsay.

Everyone who has taken a few physics or chemistry courses is familiar with Boltzmann's entropy formula,

in which S is the entropy, K_B is the Boltzmann constant (1.38062 x 10^-23 joule/kelvin), and Ω is the number of states accessible to the system. This equation is actually a simplification of the Boltzmann-Gibbs entropy when every state has the same probability p_i; viz,

These equations define a maximum entropy, since the equal probability means that you can stuff an atom or molecule into any accessible state.

At this point, we might wonder what will happen when some states are correlated with each other, a condition for which the entropy will be less than the maximum. That's what Tsallis did in a 1988 paper[1] in which he defined what's now known as the Tsallis entropy, S_q, given by the following equation:

in which the parameter, q, is called the entropic-index. This equation becomes the Boltzmann-Gibbs entropy equation when we take the limit as q approaches one. It's been a while since I did limits in Calculus, so I'll just take this on faith.

There are presently 69 papers posted on arXiv having "Tsallis entropy" in their titles. What's so important about Tsallis entropy? Boltzmann entropy applies only to systems in equilibrium, and the Boltzmann entropy is an extensive function; that is, it depends on how much matter we have in our system. In non-equilibrium systems we need another way to look at entropy, and now we have Tsallis entropy, which is non-extensive. As can be imagined, a lot of people have a problem with a non-extensive entropy.

Constantino Tsallis in February, 2010 Tsallis is at the Centro Brasileiro de Pesquisas Físicas (Brazilian Physics Research Center) (Photograph by Maria Aparecida, via Wikimedia Commons.)

Tsallis entropy has been shown to produce better results than Boltzmann entropy for the analysis of some systems in biology, nuclear physics, finance, music, and linguistics; and the correlations in DNA sequences.[2] Despite these successes, there's been criticism that the entropic-index q acts merely as a fitting parameter. There's also an argument that Tsallis entropy violates the zeroth law of thermodynamics. That's the law that states that systems in thermal equilibrium with another system are in equilibrium with each other.[3]

In the end, it appears that physicists just need to know whether to apply one entropy or another to a given system. It's not unlike knowing that you should use classical mechanics for bowling balls and quantum mechanics for atoms.[3]

References:

1. Constantino Tsallis, "Possible generalization of Boltzmann-Gibbs statistics," Journal of Statistical Physics, vol. 52, nos. 1-2 (July, 1988), pp. 479-487.
2. H. V. Ribeiro, E. K. Lenzi, R. S. Mendes, G. A. Mendes, and L. R. da Silva, "Symbolic Sequences and Tsallis Entropy," arXiv Preprint Server, January 16, 2014.
3. Jon Cartwright, "Roll over, Boltzmann," Physics World, May, 2014, pp. 31-35.