Tikalon Header

Heronian Triangles

July 25, 2014

The Greek philosophers contributed much to our understanding of the world. Archimedes (c. 287 BC - c. 212 BC) was one such philosopher who wasn't content with just understanding nature. As an inventor, he wanted to harness the laws of nature for the benefit of his fellow man. One of his inventions, still in use today, is the screw pump.

De Schroef van Archimedes, a 1993 sculpture by Tony CraggLoch Ness Monster?

The Screw of Archimedes (De Schroef van Archimedes), a 1993 sculpture by Tony Cragg in 's-Hertogenbosch, The Netherlands.

(Photograph by Polleket, via Wikimedia Commons.)

Hero of Alexandria (c. 10 - 70 AD; more properly, Heron) was another such philosopher-inventor. I wrote about Hero's inventions in a previous article (Steam Power, January 28, 2011). The most famous of these inventions, his steam engine, known as an Aeolipile, was published in his book, Pneumatica. This steam engine, although primitive, predates James Watt by seventeen centuries.

Heron of AlexandriaHero of Alexandra

The proper transliteration of Hero's name from the Greek would be Heron, but he's known as Hero.

(Illustration from the Codex of San Gregorio de Nizance, a ninth century Greek manuscript, via Wikimedia Commons.)

The philosopher title was a catch-all for intellectuals of his period, but Heron was both a mathematician and an early example of an engineer. Heron's description of the Aeolipile included an "engineering drawing" and directions for building the device.[2] The Pneumatica contains 78 devices based on physical and mechanical principles. Not all of these were his own inventions, but he didn't distinguish which were. The Roman author, Vitruvius, wrote about a steam engine built earlier by Ctesibius (285-222 BC).[3]

Most of Heron's books are written as if they were lecture notes for courses he may have taught in science, engineering and mathematics. Heron could be called the "Father of STEM." In mathematics, he's most famous for Heron's formula, a simple formula appearing in his Metrica (c. 60 AD) for calculating the area of an arbitrary triangle from the length of its sides.

As any high school student knows, the right angle seems to rule Euclidean geometry. You learn how to find the area of right triangles; and, the areas of other triangles and the trapezoid are found by decomposing them into right triangles. Heron's formula is unique, since right angles are not involved; except, of course, in its proof. Since Heron was a teacher, and his books are more like lecture notes, it's quite possible that he didn't discover this formula, but his name is linked to it, nonetheless.

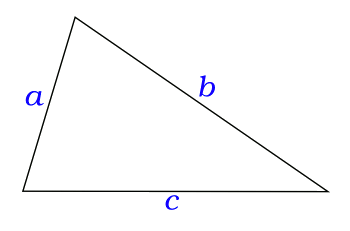Acute scalene triangleAn acute, scalene triangle with sides a, b, and c.

(Illustration by the author using Inkscape.)

With reference to the above figure, Heron's formula for the area A of a triangle with sides a, b, and c, is simply,
Heron's formula
Where the parameter, s, known as the semiperimeter, is half the perimeter; viz.,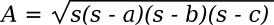
Semi-perimeter
The formula can be written in terms of the sides, only, as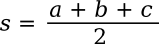
Heron's formula
Mathematicians are creative individuals, and when they see something this simple, they immediately find ways to build something more complex out of it. So, the idea arises as to what integer sides will yield an integer area. Such an object is called an Heronian triangle, and these triangles are sometimes generalized to those for which the sides and areas are rational, not just integers.

If the triangle is a right triangle whose sides are a Pythagorean triple, it's a Heronian triangle. This follows from the sides being integers and the formula for the area of a right triangle. The area must be an integer, since at least one of the non-hypotenuse sides of such a "3-4-5" triangle must be even.

Sascha Kurz of the Department of Mathematics, Physics and Informatics, the University of Bayreuth, has posted an article about Heronian triangles on arXiv.[5] This is a version of a paper published in 2008 in the Serdica Journal of Computing.[6] Kurz' paper addresses the discovery of Heronian triangles by computation.

The following table is a selection of just those Heronian triangles with greatest common divisor of one, and areas from 250-300.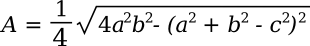
AreaPerimeterabc
25284353415
25298454013
25214470659
26496443715
264132653433
270108522927
288162806517
300150745125
I don't know whether it's proven that there are an infinite number of such triangles, but it's likely that there are, and that this is a simple proof. Alas (or, happily), I'm not a mathematician, so these things don't keep me awake at night. Kurz gives a example of a very large Heronian triangle of area 75,954,096, for which (a,b,c) = (14962,13666,11700).

The area and perimeter of the 354 "primitive" Heronian triangles (those whose sides have a greatest common divisor of one) with largest side up to 500 are plotted in the following graph. These data were calculated with my own C-language program, whose source code is found here.

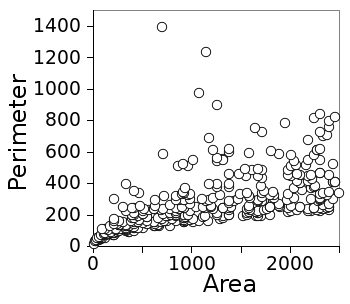Perimeter vs area for Heronian trianglesPerimeter vs area for Heronian triangles, as calculated by the author's program.

There's a wide range of perimeters consistent with a given range of areas.

(Graphed by the author using Gnumeric.)

As the graph demonstrates, there's a wide range of perimeters consistent with a given range of areas. It would be interesting to see whether this "noise" might have application in cryptography. However, the calculations are likely too computing intensive to make this worthwhile.

References:

  1. Steam Engine Library, University of Rochester Collection at the Hopkin Thomas Project, himedo.net.
  2. Bennet Woodcroft, Translator, "The Pneumatics of Hero of Alexandria," Taylor, Walton and Maberly (London, 1851).
  3. Amelia Carolina Sparavigna, "Water, air and fire at work in Hero's machines," arXiv Preprint, January 18, 2011.
  4. Sascha Kurz, "On the generation of Heronian triangles," arXiv Preprint Server, January 11, 2014.
  5. Sascha Kurz, "On the generation of Heronian triangles," Serdica Journal of Computing, vol. 2, no. 2 (2008), pp. 181-196. A PDF copy is available, here, also.