Vortex Loops

March 11, 2013

When I starting working in industrial research, more than thirty years ago, about one in five of my colleagues were tobacco smokers. Everyone of them was smart enough to know that smoking was harmful to their health, and every year the number of smokers was reduced. One year, there was a betting pool among a few smokers to determine who could refrain from smoking the longest. The winner got a little money, but he started smoking again shortly thereafter.

When I left the labs after thirty years, not a single person was a smoker. The health benefit was an obvious motivation, but numerous obstacles were imposed over the years. No smoking was allowed in any corporate building, and any outside smoking was not allowed within thirty feet of a building entrance. Perhaps it should have been thirty meters for the research buildings.

When I was younger, I would see a few skilled smokers blowing smoke rings. There were even television cartoons, so old that they were in black and white, showing a cartoon character blowing smoke rings. Nowadays, a smoke ring is an uncommon sight. Just as for coffee rings, there's a bit of physics behind smoke rings, more properly called vortex loops, since they exist in more media than smoke in air.[1-3] I wrote about coffee rings in a recent article (Coffee Ring Physics, February 11, 2013).

"Wreaths of Tobacco Smoke" by Adriaen Brouwer (1605-1638) Brouwer was a Flemish painter who apparently spent much of his time in alehouses. Notably, Rembrandt and Rubens possessed a number of his works, and his art was popular enough to be counterfeited in his own time. (From the article, "Studies of Vortex Rings" by Andrien Guébhard, in The Popular Science Monthly, vol. 20, p. 176, via Wikimedia Commons.)

The movement of a vortex loop is real. It's not like a wave, the motion of which is only apparent. As can be seen in the example of a smoke ring, the entrapped particles in the vortex travel farther than if they were just in a cloud. This long distance movement is enabled by the rolling interface between the loop and the surrounding fluid, since a vortex loop is a tube of fluid, spinning on the tube axis. The movement is usually in the direction orthogonal to the plane of the loop.

Vortex loops interested William Thompson (Lord Kelvin) in the mid-nineteenth century as a way to explain atoms. He conjectured that atoms were knotted loops of the Aether, with the number and type of knot giving the elements their particular properties.[2] The vortex loop atomic theory was wrong, but it inspired research on vortices. Hermann von Helmholtz published a mathematical analysis of vortex loops in 1858.[4]

Although linked and knotted vortex loops have been described in theory since that time, they had never been created in the laboratory. Physicists from the University of Chicago have now developed a technique for generation of vortex loops, including knotted loops, in a water tank.[1-3] Their apparatus is quite ingenious, as the photographs, below, show. The loops are generated by the rapid movement of gas bubble coated airfoils in water.

Electrolytic generation of microbubbles. Some of the hydrogen and oxygen bubbles stick to the airfoil to allow vortex loop creation. (Still image from a YouTube Video by UChicago Creative/Robert Kozloff/University of Chicago.)

Postdoc Dustin Kleckner holding a 3D-printed loop airfoil. (Still image from a YouTube Video by UChicago Creative/Robert Kozloff/University of Chicago.)

The airfoils are created using a 3D printer, and they become coated with microbubbles of hydrogen and oxygen generated by the electrolysis of water. The 3D printing proved invaluable, since it took many iterations of airfoil shape to generate the desired vortices.[1] When subjected to a 100 g acceleration, the bubbles detach from the airfoil and produce a propagating vortex loop, which is tracked with a high speed camera (see figure).

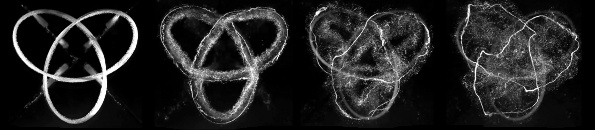Temporal evolution of an air bubble vortex loop in water. The first frame shows the initial state after detachment from the airfoil. (Still images from a Robert Kozloff/University of Chicago video.)

These experiments have yielded interesting results. Dustin Kleckner, a postdoctoral scientist at the James Franck Institute of the University of Chicago and coauthor of the vortex studies, notes that vortex knots, once thought to be persistent and stable, are not.

Says Kleckner, "They seem to break up in a particular way. They stretch themselves, which is a weird behavior."[2] Their decomposition culminates in reconnection events in which parts of the vortices annihilate each other to produce unknotted loops from those that were originally knotted.[2]

Knotted structures are thought to occur in turbulence, plasmas, fluids, both quantum and classical, and superfluids, but are nearly impossible to observe.[1-2] In many systems, the degree of knottedness has been thought to be a conserved quantity, and these experiments have shown that this might not always be the case.[2]

These results are published online in Nature Physics in an article notable for its many freely-available supplementary videos.[1] This research was funded by the Alfred P. Sloan Foundation, the Packard Foundation, and the National Science Foundation.[2]

References:

1. Dustin Kleckner and William T. M. Irvine, "Creation and dynamics of knotted vortices," Nature Physics, Published Online March 3, 2013, doi:10.1038/nphys2560.
2. Steve Koppes, "Vortex loops could untie knotty physics problems," University of Chicago Press Release, March 4, 2013.
3. Daniel P. Lathrop and Barbara Brawn-Cinani, "News and Views - Fluid dynamics: Lord Kelvin's vortex rings," Nature Physics, Published Online March 3, 2013, doi:10.1038/nphys2577.
4. H. von Helmholtz, "On Integrals of the hydrodynamical equations, which express vortex-motion," (1867 English Translation of original 1858 paper), Philosophical Magazine, Series 4 (1851–1875), vol. 33, no. 226.