Tikalon Header

The Twin Prime Conjecture

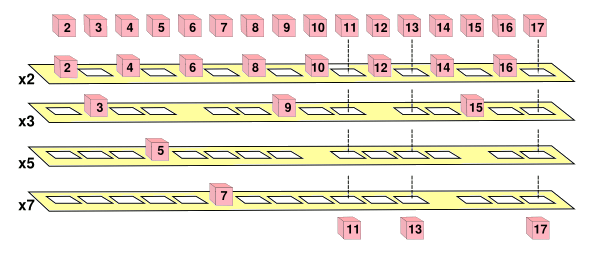
June 3, 2013

One of my most prized books as a child was the Giant Golden Book of Mathematics, written by mathematician, Irving Adler.[1] This book was nicely illustrated by Lowell Hess, who illustrated quite a few children's books in his career.

One illustration I remember from that book was the sieve of Eratosthenes, shown as an actual mechanism for filtering numbered cubes to find the prime numbers. The following figure illustrates such a mechanism.

The sieve of Eratosthenes, illustrated as a physical mechanism.
The sieve of Eratosthenes, illustrated as a physical mechanism. The first platform has holes cut to stop all numbers divisible by two, and pass all others. The second platform catches all numbers divisible by three, etc. The prime numbers are the first number stopped on each level. Since the first platform catches all even numbers, platforms to stop numbers divisible by four, six, and all other even numbers, are not included. (Illustration by the author using Inkscape.)

A prime number is any natural number greater than one with no positive divisors aside from itself and one. All other natural numbers are composite numbers, which are constructed by multiplying prime numbers together. A theorem with the impressive title, the fundamental theorem of arithmetic, asserts that any natural number greater than one can be expressed as a product of primes in just one way; so, 54 is just 2 x 2 x 13, and it can't be expressed by any other combination of primes.

One thing you notice is that one is not a prime number. If it were, composite numbers could have an infinite number of prime factors, since we can just multiply by as many ones as we desire. Thus, 54 would be 1n x 2 x 2 x 13, where n can be any integer. Also, two is prime, since that's the only way we can construct the even numbers. It's the only even prime number.

The fundamental theorem of arithmetic has been proven, but there are many unproven conjectures involving the prime numbers. Goldbach's conjecture states that any even integer greater than two can be expressed as the sum of two primes. Computers have enabled experimental mathematics, and they've given substantial credence to this conjecture, since no counterexample has been found up to 4 x 1018. Anecdotal evidence, however, is not proof, so mathematicians are still examining this conjecture.

Examination of any list of prime numbers illustrates that they become rare as we go to larger numbers. This behavior has been quantified by the prime number theorem, which states that the probability that a number N is prime will closely follow the function 1/ln(N).

Wikipedia lists 29 prime number conjectures, one of which, the first Hardy–Littlewood conjecture, gives us the mysterious twin prime constant,
.6601618158468695739278121100145557784326233602847334133...,
also known as sequence A005597 in the On-Line Encyclopedia of Integer Sequences (OEIS). This constant relates to numbers known as the twin primes.

Twin primes are prime numbers that differ from each other by the smallest possible interval; namely, two. Thus, (3,5) and (5,7) are twin primes, as are (617,619) and many others. OEIS sequence A077800 is the list of twin primes. According to Wikipedia, there are 808,675,888,577,436 twin prime pairs below 1018.

The density of prime numbers decreases as numbers get larger, so the density of twin primes decreases as well. An open problem is whether twin primes exist when we reach arbitrarily large numbers. The twin prime conjecture is that there's an infinite number of twin primes. Euclid, the famous Greek geometer, is the supposed author of this conjecture, which makes it one of the oldest conjectures in number theory.[2]

Euclid, from a 15th century manuscriptEuclid, from a 15th century Latin manuscript entitled, "Artes Liberales" (The Liberal Arts).

(Via Wikimedia Commons.)

Recent work by mathematician, Zhang Yitang, of the University of New Hampshire (Durham) has produced a result that's the closest yet to a proof of this conjecture, but still far from the mark.[2-4] As an example that mathematics sometimes works in strange ways, what's been proven is that there are infinitely many primes which differ in distance by at most 70 million. Seventy million, of course, is quite a ways from two, but Zhang's result shows that this conjecture can be addressed. Zhang's proof will appear in the Annals of Mathematics.

This proof advances the status of the twin prime conjecture beyond a result obtained a few years ago that there is an infinite number of prime pairs, but only if another unproven conjecture is true.[2-5] That proof showed that there will always be a pair of primes which are closer together than the average gap between primes anywhere on the number line.[3] Zhang was able to prove his result using standard mathematical techniques, so it was something that others could have done before, but they hadn't. Zhang thinks that his techniques can be used to push his 70 million limit downwards.[2]

As is common in creative endeavors, such as science and mathematics, individuals will carry a problem around with them for years and make no progress towards a solution; then, suddenly, the answer comes in a flash of inspiration. Zhang thought about the problem for three years, but it was only on holiday at a friend's house, during a short wait before leaving for a concert, that the solution came to him.[3] Says Daniel Goldston, a number theorist at San Jose State University,
"It's one of those problems you weren't sure people would ever be able to solve.[3]

References:

  1. Irving Adler (Author), Lowell Hess (Illustrator), "The Giant Golden Book of Mathematics [Hardcover]," Golden Press, first edition 1958, 92 pages.
  2. Maggie McKee, "First proof that infinitely many prime numbers come in pairs," Nature News, May 14, 2013.
  3. Erica Klarreich, "Unheralded Mathematician Bridges the Prime Gap," Simons Foundation Press Release, May 19, 2013. Same article on Wired.
  4. Kenneth Chang, "Solving a Riddle of Primes," The New York Times, May 20, 2013.
  5. Daniel A. Goldston, János Pintz and Cem Y. Yíldírím, "Primes in tuples I," Annals of Mathematics, vol. 170, no. 2 (September, 2009), pp. 819-862.