Tikalon Blog by Dev Gualtieri

Tikalon Header

Light Speed

April 8, 2013

Eyeglasses are only possible because of refraction , the bending of light rays when they enter a medium at an angle . The refraction of a material is measured by its refractive index n, which is simply the ratio of the speed of light in a vacuum c to the speed of light in the medium v; that is, n = c/v.

Optics was the topic of the first chapter of my high school PSSC physics textbook . That may have been because optics is easy to visualize (pun intended). This bending of light rays into a medium and its relationship to the speed of propagation of a wavefront was explained in that book using an analogy of marching soldiers .

The front tier of marching soldiers enters a muddy field at an angle. At first, a single soldier at one end finds the marching somewhat difficult, and he slows down. To prevent the soldier at his back from bumping against him, he veers to one side. This continues, until we see the parade refraction in the figure below.

soldiers marching from grass into mud

A parade of soldiers being refracted at the interface between grass and a muddy field

The difficulty with most analogies is that they explains things in one sense, but they lack explanatory benefit at a deeper level.

I wasn't comfortable with this analogy in high school.

(Source image for soldier icon via Wikimedia Commons, modified.)

This behavior of light rays was quantified by Dutch astronomer and mathematician , Willebrord Snellius (1580-1626), as Snell's law (see figure). As was the custom of his time, Snellius Latinized his birth name, Willebrord Snel van Royen. Snell's law follows from Fermat's principle of least time . In mechanics , the equivalent of this principle is the principle of least action , in which we're reminded that Nature also enjoys doing things the easy way.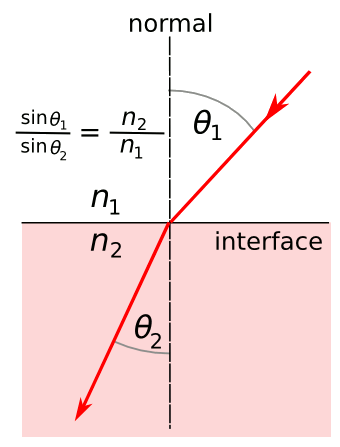

Snell's Law

Snell's Law

In most cases, the top medium is air, which has a refractive index of 1.000

The ratio of refractive indices is related to the ratio of the speed of light in the media, (n₁/n₂ = v₂/v₁)

According to Wikipedia , there's evidence that this law was first formulated by the Persian scientist , Ibn Sahl , six centuries before Snellius.

(Illustration by the author using Inkscape.)

One interesting thing about Snell's law is that there's an angle, θ = arcsin(n₂/n₁), beyond which no light is transmitted from one medium to the other. It's completely reflected , a condition called total internal reflection . This property is useful, since it allows prisms to reflect light without any reflective metal coating (usually aluminum ). It also allows an important way to couple light into liquid droplets in some sensors .

The following table lists some representative values of refractive index at visible wavelengths .

Titanium dioxide (Rutile)	2.496		Borosilicate glass (Pyrex )	1.470
Diamond	2.419		Fused silica (Fused Quartz)	1.458
Cubic zirconia	2.17		Air at STP	1.000277
Polycarbonate	1.586		Vacuum	1
Sugar solution (75%)	1.4774

The refractive index of materials varies with wavelength , becoming smaller as the wavelength increases. This change in index is very predictable, and the refractive index over a range of wavelengths can be calculated from the Sellmeier equation if the index at just a few wavelengths is known. This equation is usually written as

n²(λ) = 1 + [B₁ λ²/(λ² - C₁)] + [B₂ λ²/(λ² - C₂)]
+ [B₃ λ²/(λ² - C₃)]

For fused silica, B₁ = 0.696166300, B₂ = 0.407942600, B₃ = 0.897479400, C₁ = 4.67914826×10⁻³ μm², C₂ = 1.35120631×10⁻² μm², and C₃ = 97.9340025 μm².

I worked for several years with an optical physicist who was tasked with making accurate thickness measurements for thin crystal films I prepared in my laboratory . Not a day would pass when he didn't mention the Sellmeier equation.

That was the time when general purpose computers were just being integrated into laboratories, and he had an automated system for film thickness measurement based on optical interference . Accurate refractive index values over a wide range of wavelengths were needed for his calculations. The utility of the Sellmeier equation can be seen in the following figure.

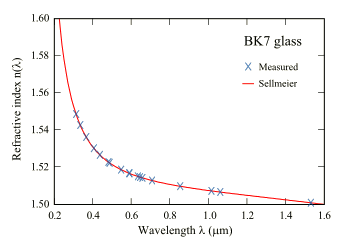$Refractive index of BK-7 glass and its fit to the Sellmeier equation$

The refractive index of BK7 glass over a wide range of wavelengths, and the Sellmeier equation fit to the data.

The agreement is excellent.

(Wikipedia image by Bob Mellish.)

Refractive indices are referenced to the vacuum. As I've written in the context of the Casimir effect (Not So Empty Space, July 23, 2008 ) the vacuum is not really empty space. Empty space is only empty when averaged over a period of time. At any instant, it's a sea of virtual particles coming into and out of existence. Physicists are now considering the possibility that the speed of light we measure is an average value. It will show variation over very short length scales.[1-7]

Physicists from the Université Paris-Sud (Orsay, France), the Université Paris Diderot (Paris, France), the Max-Planck-Institut für die Physik des Lichts (Erlangen, Germany), the Universität Erlangen-Nürnberg (Erlangen, Germany) and the Universidad Complutense (Madrid, Spain) have published two papers in the European Physical Journal about this concept.[2,4]

One paper shows the possibility that the vacuum permeability , μ_o, a magnetic constant, and the vacuum permittivity , ε_o, an electrical constant, may arise from the polarization and magnetization of continuously appearing and disappearing fermion pairs of the virtual particle sea.[2,3] Light, which is an electromagnetic wave , would interact with these particles in a granular fashion at the Planck scale , so its speed would vary. All such interactions average out at larger length scales to give us the speed of light we measure.[2,3] The time scale for such fluctuation is estimated to be about 50 attoseconds , so an experimental test might soon be possible.[1]

The other paper uses this idea to estimate the total number of charged elementary particles in nature. They calculate that the vacuum impedance arises from the charges of the virtual particles, and they predict that the total number of charged elementary particles is about a hundred.[1,4-5]

References: