Tikalon Blog by Dev Gualtieri

Evaporation

August 7, 2013

One bit of physical chemistry that most children learn at a very young age is that liquids evaporate more quickly on hot days than cold days. That observation might come from noticing that a splash of beverage spilled on a shirt dries quickly in the summer ; or, seeing how fast a sidewalk dries after a summer's rain . The really observant child, one destined to become a scientist , might even notice that the evaporation rate depends on wind speed .

Thermodynamically , both the thermal and wind-driven processes are easily understood. The wind drives away vapor molecules that linger just above the liquid, so it makes the air less saturated with the liquid molecules. Equilibrium at the liquid-air interface means that the same number of molecules leave the liquid to become vapor as those condensing from the vapor to form more liquid. The wind shifts the equilibrium towards more evaporation.

The temperature effect is quantified by the Clausius–Clapeyron equation , which relates how the vapor pressure of a liquid changes with temperature from an initial state (1) to a final state (2); viz.,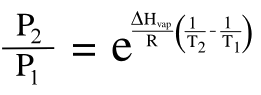

where ΔH_vap is the enthalpy of vaporization , R is the gas constant (8.314 J K ⁻¹ mol ⁻¹), P is the pressure and T is the absolute temperature . The exponential term means that even a modest temperature change will cause a large change in vapor pressure. The vapor pressure of water (ΔH_vap = 40.68 kj/mol) at 25 °C will be 30% larger than that at 5 °C.

Scientists from the Institute of Physical Chemistry of the Polish Academy of Sciences (Warsaw, Poland ) have just completed a study of evaporation of liquid droplets over a wide range of droplet sizes. Their results are published in the journal, Soft Matter .[1-2] In good scientific form, some of their experiments had droplets evaporating, not in air , but in an inert gas .

Research at the Institute of Physical Chemistry, the Polish Academy of Sciences, shows that temperature differences as small as 0.0001 kelvin drive droplet evaporation.

(IPC/PAN photograph by Grzegorz Krzyzewski.)[2]

The Clausius-Clapeyron equation is derived from equilibrium thermodynamics where it's assumed that molecules can attach or detach from the fluid with ease to enter the vapor phase. It's also assumed that the liquid and the vapor are at the same temperature, although evaporation will cool water . The overall principle is that the evaporation happens slowly enough that the temperature equilibrates.

The Polish group attacked the problem of droplet evaporation using a computer model and validating experiments . The computer model was a molecular dynamics simulation of a two-component fluid in which molecular interactions were via a Lennard-Jones potential . The purpose of the simulation was to calculate the energy flux between the liquid droplets and the surrounding atmosphere.[1] Droplet size extended down to nanoscale dimension .[2]

In the experiments, microdroplets were held in an electrodynamic trap where they were studied as they evaporated. This was like a Millikan oil drop experiment in which the drops evaporated. Studied systems were water evaporating in air, glycol and glycerol into nitrogen , and argon into argon vapor.[2]

Simplified schematic diagram of the Millikan oil drop experiment . The voltage is adjusted to keep a droplet floating in the region between the plates. (Modified illustration from Wikimedia Commons.)

There's a boundary layer between the liquid and vapor that's thermally insulating , and this layer limits the heat flux. The thickness of this boundary layer was found to depend primarily on the conditions in the environment and it's not related to the droplet size. For this reason, nanometer-sized droplets evaporate more slowly than expected, essentially because the interface has few molecules, and the heat flux is by radiation , and not by mass transfer .[2]

What was found in the experiments was a clear difference in temperature between droplets and the surrounding atmosphere, and that the pressure remained constant during evaporation. The droplet temperature appears to be the prime factor in droplet evaporation.[2] Says Daniel Jakubczyk, a coauthor of the paper,

"Evaporation turns out to be a process driven by very small temperature differences. Often, only ten-thousandth parts of kelvin are enough to make it happen!"[2]

The experimental conditions of different liquids and varied droplet sizes over three orders of magnitude resulted in evaporation times from seconds to tens of minutes.[1] The model equation derived from these observations gives good results over this wide range of conditions; that is, it appears to specify a universal law.[1] As Marek Litniewski, another study coauthor, summarized,

"Small droplets can evaporate within nanoseconds, whereas large drops need up to a few tens of minutes. The experiments confirmed that in spite of such a large time span, extending over a dozen of orders of magnitude, our formula correctly describes the kinetics of all these processes."[2]

This research can be applied to some currently important areas, such as the contribution of water evaporation to climate change . Water vapor is Earth's primary greenhouse gas . It may also lead to the design of better fuel injectors to increase internal combustion engine efficiency .[2] This work was funded by the Polish Ministry of Science and Higher Education .[2]

As for drops of a different genre , "Drops of Jupiter (Tell Me)" is a popular song by the American musical group, Train . It was released in 2001, but it still has frequent airplay , today.[3]

Evaporation

References: