Tikalon Blog by Dev Gualtieri

Tikalon Header

Entangled

May 22, 2012

About a year ago, I saw a cute, feature length, animated film called Tangled .[1] This was a Disney retelling of Rapunzel , a Grimm Brother's fairy tale . The purported reason for naming the film, Tangled, and not Rapunzel, was to address the larger children's market (myself included?), and not have this become another little girls' princess movie.

Indeed, the plot deviates so sharply from the original fairy tale, that calling it Rapunzel would have been a misnomer. In any case, this film made many young girls very happy, and it made a lot of money for Disney. I enjoyed it, too.

The word, tangle, relates to one thing twisting around itself; while the word, entangle, is used when separate things twist around each other. There are quite a few physics papers published about the idea of entangled quantum states . Nowadays, it's easy to entangle a pair of photons and send one of them a long distance in an optical fiber .

Quantum mechanics gives us answers that are not intuitive to our macroscopic existence. Each member of an entangled pair will have indefinite spin , for example, that's finally resolved in a measurement. The quantum strangeness in entanglement (what Einstein called, "Spooky action at a distance") is that a measurement of your local photon tells you what the result will be if the measurement is done on the distant photon.

In theory, this is true even if these photons are at opposite sides of the universe . Wikipedia , my information companion , makes the understatement that "... there is some debate about a possible underlying mechanism that enables this correlation to occur even when the separation distance is large."[2]

In a previous article (Rolling Rubber Bands, August 13, 2010), I wrote about a simple type of entanglement; that involving the everyday, macroscopic, definitely not quantum-regime, objects, rubber bands . A research team from MIT and the École Polytechnique (Paris ) found that rolling circular rubber bands, when forced to roll at high speeds, become more peanut-shaped . When a critical speed is reached, the upper and lower portions of the loops came into contact, and the bands jump off the surface.[3-5]

Figure caption

I would often use rubber bands to hold my experimental apparatus together, but they can be useful objects of an experiment, also.

(Photograph by Bill Ebbesen, via Wikimedia Commons).

A team of physicists , and a mechanical engineer , from the Georgia Institute of Technology (Atlanta, Georgia), and a physicist from the Rochester Institute of Technology (Rochester, New York) have decided that their fastener of choice is not the rubber band, but a staple . They investigated how the shape of staples, and their resultant proclivity for entanglement, affects their properties as a granular ensemble .[6-8]

For starters, they decided that staples are a better object of study than spherical cows , since "Many living and nonliving materials are composed of ensembles of non-spherical particles."[6,8] There have been many studies on things such as sand grains , but not much on concave shapes that interlock.[7] Their experiments show effects similar to those observed in studies of wet, cohesive granular materials.[6,8]

The staples were made of steel (density, 7.85 g/cm), and they were of constant width, but varied length. The staples had a square cross section of 0.5 mm, and the length/width ratios were between 0 and 1.4. Heaps of such staples were automatically shaken in a cylindrical vessel, and column collapse was monitored using a digital camera .

It was found that column collapse occurs at a time τ that's given by

τ ∝ exp(Γ/Δ)

where Γ is the peak acceleration of the sinusoidal vibration , and Δ resembles an activation energy .

Piles of staples with the intermediate length/width ratio of 0.4 took the longest time to settle. That's because the maximum activation energy occurs at that point.[6,8] The reason for this is that there are two competing effects. Small length/width favors a higher initial packing density , while large length/width increases the number of entanglements. A balance of these two effects results in more stable piles.[7]

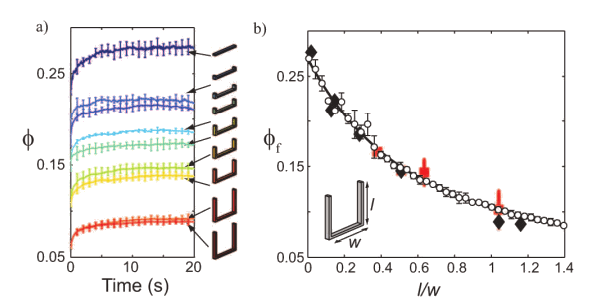Packing of shaken staples

As might be expected, staples with no prongs settled into piles of the highest packing fraction φ. (Fig. 2 of ref. 6, edited).[6]

How can we talk about staples without a mention of the famous red stapler in the 1999 film, Office Space (Mike Judge , Director).[9] The film's writer and director, Mike Judge, has a Bachelor of Science degree in physics from the University of California, San Diego .

References: