Tikalon Blog by Dev Gualtieri

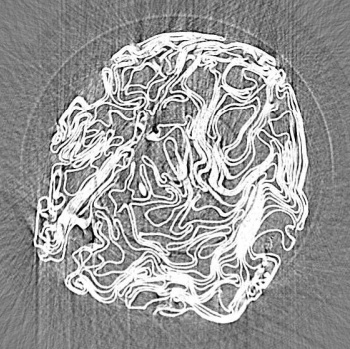
Crumpling

August 27, 2012

I'm often surprised by the quantity of items that arrive in my (snail mail ) mailbox . Along with the usual aggregate of bills , there's a stream of coupons , postcard advertisements , tabloids of supermarket specials, and catalogs . The Internet has only slightly diminished this steam of paper , and there are forces at work to that perpetuate its existence.

My supermarket will only accept printed coupons, and not coupons presented on a smartphone . Most of the reduction in my mail has come from my getting content online, rather than through trade magazines ; and using online search, rather than electronic component catalogs.

The interesting thing about all this is that I never really notice the paper. All my attention is directed to what's printed on it. Marshall McLuhan may have famously stated that "the medium is the message ," but this is a counterexample . However, the true McLuhanite might say that the medium does play a part, since the paper coupons are sized to fit my pocket, and the tabloids unfold to a larger size that takes control of our entire field of vision .

There's a lot of physics in a sheet of paper, especially when it's crumpled. I wrote about crumpling in two previous articles (Crumpled Paper, October 25, 2011 , and Paper Chase, September 7, 2010 . Physicists started to investigate crumpling of sheets of paper and other materials about a decade ago, and they found some universal laws .

In the mid-1990s, Eric M. Kramer and Alexander E. Lobkovsky of the James Franck Institute and the Department of Physics of the University of Chicago recorded the emitted sound during crumpling of crumpled Mylar sheets. When analyzed in small time slices, the acoustic emission is a series of discrete clicks.[1-2] Sound amplitude is related to energy , and these experiments showed that the energies of the clicks were distributed according to a power law distribution .

P(E) ∼ e^-α

where P(E) is the probability of a click having energy E, and α is about one. The power law didn't change when the sheet material or size of the sheet was changed, so it's a universal law. The Chicago experiments showed the validity of this law over six orders of magnitude .[3]

X-ray tomograph section of a compressed aluminum foil ball.

This image was constructed from a thousand projections for a ball for which the radius was compressed by a factor of six.

(Fig. 1 of ref. 4, via arXiv Preprint Server ).[4-5]

Crumpled sheets have interesting mechanical properties , as well. A typical crumpled ball of paper may be 75% air, but it's mechanically stiff , and quite a bit of force is needed to crumple it further. Crumpling a sheet that's eight times larger on a side than another sheet requires only twice as much energy, although the larger sheet has sixty four times the area of the smaller sheet. Information like this is useful if your aim is to absorb energy, as in the design of crumple zones in an automobile.

For other interesting examples, see the references.[6-8]

One thing all these experiments have in common is the random nature of the crumpling. Whenever possible, experimentalists want to take more control of their experiments. That's why physicists at the University of Massachusetts Amherst designed an apparatus that allows crumpling of ultra-thin polymer sheets (a few tens of nanometers thick).[9-12] One motivation was to provide confirmatory evidence for a crumpling model they had developed with colleagues at the Université Pierre et Marie Curie (Paris), Oxford University (Oxford, UK), and the Universidad de Santiago (Santiago, Chile). Although the theory of buckling of compressed plates was developed by Euler hundreds of years ago, this theory seems to deviate from experiment for very thin films.[13]

Their experiments involved placing circular disks of the thin polymer over a water-filled orifice . Surface tension holds the film in place as applied pressure causes a water dome to form under it, thereby crumpling the film (see figure)

A thin polymer sheet floating on a drop of water. The sheet is pulled taut from the edge of the drop orifice.

(Amherst University Image).

Before there's crumpling, there's wrinkling. The difference between these two phenomenon is the shape of the surface. There are smooth curves for wrinkling, and reentrant curves for crumpling, as can be seen in the Xray topograph, above. When the wrinkling encompasses half the sheet radius, there's a transition to crumpling that's material-independent.[11] Said Benny Davidovitch , one of the authors of the study,

When the radius of the drop gets small enough, the thin film starts to develop fine radial wrinkles near its outer perimeter as the water pressure increases. If you keep adding pressure, decreasing the radius further, a second transition takes place and the film starts to crumple and to look more like a table cloth, draping with sharp creases over the edge of a flattened top."[9]

The basis of the theory that describes this process is that the films deform in a way that reduces the compression.[9] Wrinkling is the first feature that reduces the compression, and then there's a continuous transition to a crumpled state.[11] Of course, one of the joys of experiment is that you often discover something new along with what you expected to find. The Amherst team is looking at the finer details of the crumpled features in their experiment.[9]

Crumpling

References: