
Smith Numbers
May 9, 2012 Mathematicians work with numbers like artists work with paint. Sometimes the numbers are regular, like a Josef Albers' painting. Sometimes they're as chaotic as a painting by Jackson Pollock. Sometimes they're just playful, as in the examples that I give below. One playfully constructed number is Champernowne's number, sometimes called Champernowne's constant. This number is sequence A033307 in the The On-Line Encyclopedia of Integer Sequences, started by Neil Sloane in 1964 when he was still a graduate student. It's named after D. G. Champernowne, the mathematician who published it in 1933 while he was an undergraduate student.[1] Here are it's first few digits0.1234567891011121314151617181920212223...Close inspection shows that it's just the concatenation of all the decimal numbers, which is a very arbitrary way to form a number. Since we're doing such playful things with numbers, why stop with base ten? Remembering that the numbers in base two are expressed as 1, 10, 11, 100, 101, 110, 111, etc., you can build a binary Champernowne number that looks like this,
0.11011100101110111...A palindrome is a word or phrase that's the same whether read forwards or backwards. One famous example of this is Adam's supposed first words to Eve, "Madam, I'm Adam." There are many numbers that have this same property, so writing these would be no fun at all. What's more fun is finding prime numbers with this property. These are called, appropriately, the palindromic primes. A simple example is the number eleven; a more complex one is 17471. The palindromic primes are integer sequence A002385. You can look for palindromic primes in number bases other than ten. The prime number 1991 is also a palindrome when written in hexadecimal, 7C7. These examples use very simple rules to specify unusual numbers. We can be more creative, as Ramanujan was, and form something like the taxicab numbers. G.H. Hardy mentioned in a visit to Ramanujan that he had traveled to see him in a taxicab with the number 1729, which seemed like a dull number. Ramanujan corrected him, saying that 1729 is the smallest number expressible as the sum of two positive cubes in two different ways.
1729 = 13 + 123 = 93 + 103I mentioned taxicab numbers in a previous article (Special Numbers, September 21, 2011). There's another type of number that combines some of the flavor of prime numbers with that of Champernowne's number. These are the Smith numbers, named by the inventive mathematician, Albert Wilansky, who found that the telephone number, 4937775, of his brother-in-law, Harold Smith, had an unusual property. A Smith number is a composite number for which the sum of its digits is equal to the sum of the digits in its prime factorization.[2] Just as for palindrome primes, we're not restricted to base ten. It's important to note that we're talking about the sum of the digits of the factors, not the sum of the factors, themselves. In the case of Smith's telephone number,
4937775 = 3 x 5 x 5 x 65837 (prime factors of 4937775)The Smith numbers are integer sequence A006753. It's been proven that there are infinitely many Smith numbers.[3] Here are the first fifty Smith numbers.
4 + 9 + 3 + 7 + 7 + 7 + 5 = 42 (sum of digits of 4937775)
3 + 5 + 5 + 6 + 5 + 8 + 3 + 7 = 42 (sum of digits of prime factors)
4, 22, 27, 58, 85, 94, 121, 166, 202, 265, 274, 319, 346, 355, 378, 382, 391, 438, 454, 483, 517, 526, 535, 562, 576, 588, 627, 634, 636, 645, 648, 654, 663, 666, 690, 706, 728, 729, 762, 778, 825, 852, 861, 895, 913, 915, 922, 958, 985, 1086A computer program to generate Smith numbers is very easy to write; so easy, in fact, that I offer my own source code, here. As can be seen from the two following graphs, generated by my data, the Smith numbers (at least below 10,000), on average, are rather uniformly distributed, and the gaps between Smith numbers show no apparent pattern. It would be interesting to assess the gap between Smith numbers as a noise source.
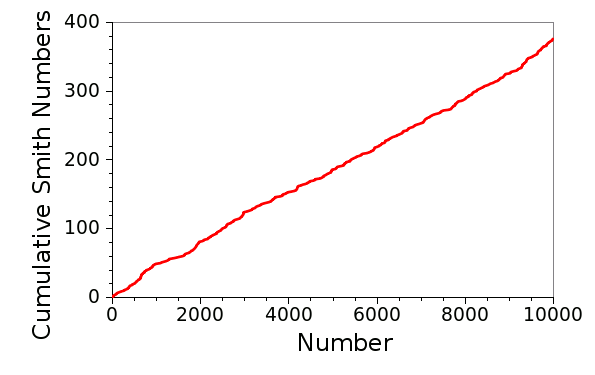 |
| Cumulative number of smith numbers below 10,000. There are 376. (Graph rendered using Gnumeric). |
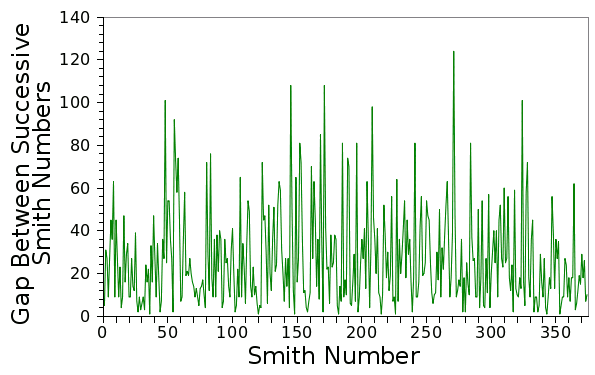 |
| Plot of the first 375 gaps between Smith numbers. (Graph rendered using Gnumeric). |
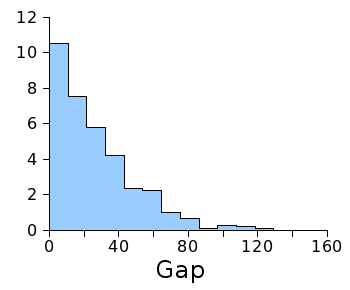 | Histogram of the first 375 gaps between Smith numbers. (Graph rendered using Gnumeric). |