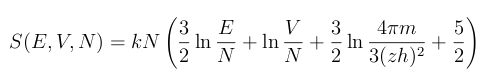Sackur-Tetrode
February 2, 2012 Whenever I hear the word, "tetrode," I think of the four-element vacuum tube by that name. This tube has four elements (tetra-, τετρα-, is the Greek prefix for the number four), but only if you ignore the filament that's required to bring the cathode to the temperature required for thermionic emission of electrons. Someone who's a little younger, and more physicist than electrical engineer, would recall the Sackur-Tetrode equation. The hundredth anniversary of the Sackur-Tetrode equation is this year.[1] | Vacuum tube nostalgia - A tetrode. The elements, from top to bottom, are the plate, screen grid, control grid, cathode and filament. Illustration by the author, rendered with Inkscape. |