Graphene Mass Standard
February 16, 2012 Mass is of fundamental importance in physics. Our system of units, now called the International System of Units (SI, for Système international d'unités), was called the MKS system, for meter, kilogram, second. The primary mission of CERN's very expensive Large Hadron Collider (LHC) is the search for the Higgs boson, the particle that's conjectured to give all other elementary particles their mass. For all the importance of mass, the method for standardizing mass is a relic of a classical physics period long passed. The present mass standard is a physical object, a cylinder of a 90% platinum - 10% iridium (by weight) alloy, the international prototype kilogram. This object, maintained at the Bureau International des Poids et Mesures (International Bureau of Weights and Measures), is lovingly compared with copies that are distributed to international weights and measures organizations for comparison against their own physical mass standards. As you can imagine, all the care in the world, and even the use of such a durable and non-tarnishing alloy, can't eliminate all errors. In fact, the catalytic action of platinum might be responsible for reactions with polluted air that add a little more mass to this object, year after year. However, the change has been small, less than 100 parts per billion (ppb), as can be seen in the graph that shows the upwards increase in mass of eleven transfer mass standards.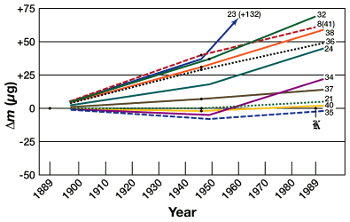 | Upwards drift of eleven international mass standards. (Via Wikimedia Commons). |
"Graphite is constructed from graphene sheets whose controlled synthesis at the atomic-scale is likely to see great progress by nanotechnologists in the years ahead. If any macroscopic object will be possible to assemble from a chosen number of atoms in the decades ahead, this may be it."Fraundorf examines the growth of graphite from a seed plane of twenty four carbon atoms, as shown in the figure. Lateral growth is accomplished by adding units to the periphery, and it can be seen that at every hexagonal edge of the ensemble there are two added atoms m for every added cell element n.
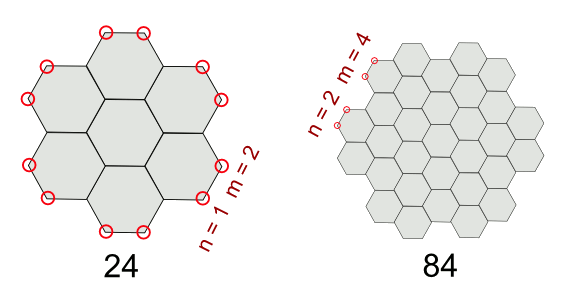Counting atoms in graphene sheets. (Illustration by author, rendered with Inkscape).
When building an hexagonal prism of graphene sheets of m layers, the number of atoms N is given by the equation,
N = 3 m2 + (9/2) m3It's possible to build a structure that comes extremely close to having an Avogadro's number of atoms, as shown in the table.
Such a graphite crystal would be about 1.71 cm high. A circumscribed cylinder around this crystal would have a diameter of about 1.45 cm. Of course, it would weigh twelve grams.
n m N 0 0 0 1 2 48 2 4 336 3 6 1080 4 8 2496 5 10 4800 6 12 8208 7 14 12936 8 16 19200 9 18 27216 10 20 37200 25,575,030 51,150,060 6.02214 x 1023