
Coupled Oscillators
November 15, 2011 Oscillation, which I reviewed in a recent article (Self-Oscillation, October 28, 2011), is one of the most important physical phenomena. Everywhere you look, things are swinging, fluttering or pulsing. Oscillators that are close in frequency can synchronize with each other if they are proximally placed to exert an influence on each other. One example of a coupled oscillator in the microscopic realm is the laser, in which the emissions of the atoms are synchronized. Christiaan Huygens was the first to observe this effect for pendulums (or, pendula, if you prefer), which are mechanical oscillators. Huygens interest in pendulums is understandable, since he was the inventor of the pendulum clock. This effect, which he called odd sympathy was described in a letter to R. Moray of the Royal Society of London. Portion of the February 27, 1665, letter of Christiaan Huygens to R. Moray describing the odd sympathy of two proximate pendulums. The letter was read before the Royal Society. (Source: Page 247 of Ref. 1).
As the letter above states, Huygens noticed the effect while lying in bed because of an illness. He found that two pendulum clocks, mounted on the same structure, would eventually synchronize in a state in which their pendulums would swing in exactly opposite directions. Huygens chose to call it odd sympathy, since the pendulums synchronized 180° out of phase.
Careful scientist that he was, Huygens tested the hypothesis that air currents from each pendulum were influencing the swing of the other, and he found that this wasn't the case. He finally decided that the pendulums caused small mechanical movements of the base, and this was the driving force for synchronization.
We can intuitively understand how this could happen. With reference to the figure, the rightwards swing of the rightmost pendulum (B) will pull the base also to the right. This will pull the pivot of the leftmost pendulum (A) to the right. Because of inertia, the bob of pendulum A will stay in place, but this is equivalent to it's moving to the left. So, movement of one pendulum bob to the right causes the second pendulum bob to move left, an odd sympathy.
Portion of the February 27, 1665, letter of Christiaan Huygens to R. Moray describing the odd sympathy of two proximate pendulums. The letter was read before the Royal Society. (Source: Page 247 of Ref. 1).
As the letter above states, Huygens noticed the effect while lying in bed because of an illness. He found that two pendulum clocks, mounted on the same structure, would eventually synchronize in a state in which their pendulums would swing in exactly opposite directions. Huygens chose to call it odd sympathy, since the pendulums synchronized 180° out of phase.
Careful scientist that he was, Huygens tested the hypothesis that air currents from each pendulum were influencing the swing of the other, and he found that this wasn't the case. He finally decided that the pendulums caused small mechanical movements of the base, and this was the driving force for synchronization.
We can intuitively understand how this could happen. With reference to the figure, the rightwards swing of the rightmost pendulum (B) will pull the base also to the right. This will pull the pivot of the leftmost pendulum (A) to the right. Because of inertia, the bob of pendulum A will stay in place, but this is equivalent to it's moving to the left. So, movement of one pendulum bob to the right causes the second pendulum bob to move left, an odd sympathy.
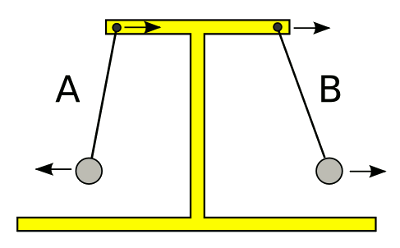 | How coupled pendulums synchronize 180° out of phase (see text). (Illustration rendered by Inkscape). |
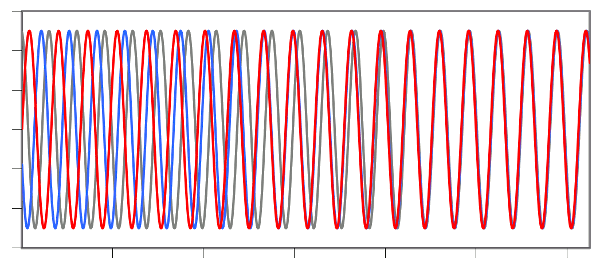 Simulation of the synchronization of three phase-coupled oscillators using (this C program). Graph rendered by Gnumeric.
Kurt Wiesenfeld, Michael Schatz and colleagues at Georgia Tech did a further study of Huygens' pendulums in 2002.[6] In particular, they examined the affect of coupling on the synchronization and found that not all double pendulums perform as Huygens found. If the coupling is too small, as when the mounting is very rigid, there will be no synchronization. In the other case of too much coupling, the pendulums have large changes in their swing amplitude, one pendulum has too small of a swing to engage its escapement, and it stops.[7]
The Georgia team's mathematical analysis showed that pivot friction is the root cause for the maintenance of the antisynchronized motion. When the pendulums are swinging with the same amplitude in opposite directions, the mounting beam doesn't move, since their forces cancel. This minimizes the pivot friction, so it's the lowest energy state.[7]
Coupled oscillators have even been used to model the response of the supply-demand interaction in economics to fluctuations in supply or demand.[8] And, how can I resist mentioning that Synchronicity is the name of the final studio album by The Police, released in June, 1983.
Simulation of the synchronization of three phase-coupled oscillators using (this C program). Graph rendered by Gnumeric.
Kurt Wiesenfeld, Michael Schatz and colleagues at Georgia Tech did a further study of Huygens' pendulums in 2002.[6] In particular, they examined the affect of coupling on the synchronization and found that not all double pendulums perform as Huygens found. If the coupling is too small, as when the mounting is very rigid, there will be no synchronization. In the other case of too much coupling, the pendulums have large changes in their swing amplitude, one pendulum has too small of a swing to engage its escapement, and it stops.[7]
The Georgia team's mathematical analysis showed that pivot friction is the root cause for the maintenance of the antisynchronized motion. When the pendulums are swinging with the same amplitude in opposite directions, the mounting beam doesn't move, since their forces cancel. This minimizes the pivot friction, so it's the lowest energy state.[7]
Coupled oscillators have even been used to model the response of the supply-demand interaction in economics to fluctuations in supply or demand.[8] And, how can I resist mentioning that Synchronicity is the name of the final studio album by The Police, released in June, 1983.
References:
- M. Nijhoff, Ed., "Ouevres Completes de Christian Huygens," (Societe Hollandaise des Sciences, The Hague, The Netherlands, 1893), vol. 5, p. 247 (in French).
- Erica Klarreich, "Huygens's Clocks Revisited," American Scientist, vol. 90, no. 4 (July-August 2002).
- M. C. Cross, "Improving the Frequency Precision of Oscillators by Synchronization," arXiv Preprint Server, September 21, 2011.
- Synchronisation of 5 coupled metronomes done in Lancaster University, Physics Department, YouTube Video by abahraminasab, December 18, 2007.
- Two pendulums attached to the same horizontal string transfer their motion back and forth, YouTube Video by Fred Wittel, September 7, 2007.
- Matthew Bennett, Michael F. Schatz, Heidi Rockwood and Kurt Wiesenfeld, "Huygens's clocks," Proc. R. Soc. Lond. A, vol. 458, (March 8, 2002), pp. 563-579.
- Erica Klarreich, "Discovery of Coupled Oscillation Put 17th-Century Scientist Ahead of his Time," SIAM News, vol. 35, no. 8, October, 2002.
- Y. Ikeda, H. Aoyama, Y. Fujiwara, H. Iyetomi, K. Ogimoto, W. Souma and H. Yoshikawa, "Coupled Oscillator Model of the Business Cycle with Fluctuating Goods Markets," arXiv Preprint Server, October 31, 2011.
- M. C. Cross, "Improving the Frequency Precision of Oscillators by Synchronization," arXiv Preprint Server, September 21, 2011.