Tikalon Blog by Dev Gualtieri

Tikalon Header

Maxwell's Other Equations

April 6, 2011

There's going to be a lot of press this year about James Clerk Maxwell , since it's been 150 years since the publication of Maxwell's equations of electromagnetism .[1-2] These short equations, as now written in the nomenclature of a more modern physics , are enough to make a physicist cry; but there are two types of tears. The older professors are brought to tears because of the beauty of the equations, and the younger students are crying when they discover that they need to make sense out of these arcana . This is one case in which Wikipedia , although much beloved by this author, won't be of much help.

Maxwell's principal discovery was the idea that light is an electromagnetic wave . Building on Faraday's earlier demonstrations that an electric current (a movement of charges ) will generate a magnetic field ; and a changing magnetic field will cause a current that also causes a changing electric field, Maxwell had the idea that electricity and magnetism could feed on each other in a bootstrap of co-creation . A time-varying electric field would create a time-varying magnetic field, and this resulting object is a light wave.

The importance of an idea can be seen in the number of times that it's reused. John Archibald Wheeler invented a bootstrapped object he called the geon . A geon is an electromagnetic (or gravitational ) wave which holds itself together in a small region of space because of the gravitational attraction of its own field energy . Wheeler thought this could be a model for elementary particles , although it's still not known whether such objects would be stable. The same problem existed for the electron before quantum mechanics . According to classical theory, electrons are not stable, since they would radiate energy in their orbit around the nucleus, finally spiraling into it.

Figure caption

John Wheeler autographed one of his books[3] for me in March, 2000. As you can see, Wheeler, who lived in the years 19xx for 88 years of his life, was still not accustomed to Y2K.

Maxwell was also fond of statistical mechanics , as the Maxwell–Boltzmann distribution demonstrates, and there are some other Maxwell equations that are not the ones that are being celebrated. These equations, which are now denigrated to being merely Maxwell's relations , involve all the important thermodynamic quantities; and, like one form of his electromagnetic equations, these are differential equations , as shown below.

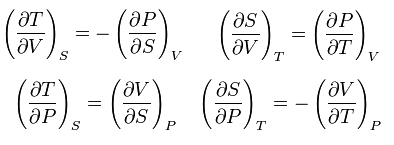Maxwell's Thermodynamic Equations

Maxwell's Thermodynamic Equations.
(Modified, from Wikipedia )

These equations involve the three quantities with which Boyle would be familiar, pressure (P), volume (V) and temperature (T); and they include entropy (S). The equations are obtained through manipulation of the equations involving the thermodynamic potentials ; namely,

dG = -SdT + VdP
dH = TdS + VdP
dU = TdS - PdV
dA = -SdT - PdV

Theses equations relate the Gibbs free energy (G), enthalpy (H), Helmholtz free energy (A) and the system internal energy (U) to measurable quantities. A little mathematical manipulation gives you the following interesting relations.

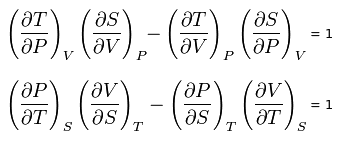Figure caption

Maxwell's Thermodynamic Equations.
(Modified, from Wikipedia )

These equations are fun to look at because of their symmetry , and they form the basis of a lot of subsequent thermodynamics. Aside from a few homework problems while I was in school, I've never used them directly; but their fingerprints are all over two of my most popular reference books.[4-5]

References: