Tikalon Blog by Dev Gualtieri

The 2011 Nobel Prize in Chemistry

October 7, 2011

The lines between scientific disciplines are not that distinct. At least on paper, I'm a materials scientist , but I've coauthored papers with physicists , electrical engineers and chemists . There's a general scientific corpus that you need to learn to become skilled in any advanced scientific field. That's why we all take many of the same courses as undergraduates . We have the example of Marie Curie , who was awarded the Nobel Prize in Physics in 1903 (for radioactivity ), and the Nobel Prize in Chemistry in 1911 (for the discovery of radium and polonium ).

This year's Nobel Prize in Chemistry could just have been awarded in physics. In fact, its crystallographic background was the subject of the award of the 1914 Nobel Prize in Physics to Max von Laue "for his discovery of the diffraction of X-rays by crystals ," and the 1915 Nobel Prize in Physics to the father-son team of William Henry Bragg and William Lawrence Bragg for the "analysis of crystal structure by means of X-rays."

The 2011 Nobel Prize in Chemistry was awarded to the Israeli , Dan Shechtman , "for the discovery of quasicrystals ."[1-7] A quasicrystal is a material that exhibits some of the properties of a crystal, such as long-range order , but its structure does not have translational periodicity . The reason that such subject matter is Nobel Prize material is that, before Shechtman's 1984 publication on his discovery, such an idea was absurd.[8] Shechtman, as sole recipient, gets the entire $1.5 million monetary award.

Although his publication was in 1984, the actual discovery was made in 1982 (see figure). It took two years for Shechtman to get his paper accepted for publication.[3] Linus Pauling , who was generally open-minded about new ideas, didn't believe that such crystals could exist, and he searched for methods by which crystallographic defects could give the same result.[2]

Shechtman was finally able to get his work published by adding a corp of respectable coauthors: Ilan Blech, a materials scientist, Denis Gratias, a crystallographer, and John Cahn , a physicist at NIST .[8] Shechtman was working on a NIST project while on sabbatical at Johns Hopkins University .[2] Said Cahn, "All I did was present the wonderful work that he had done in a compelling way."[3]

After publication, however, numerous other examples appeared, in alloys of aluminum , copper , and iron ; and of ytterbium and cadmium .[7] There was even one natural source, an alloy of aluminium, copper and iron supposedly excavated from rocks in the Koryak Mountains in Russia .[3] The name, quasicrystal, was used by other authors, and the name stuck.[9]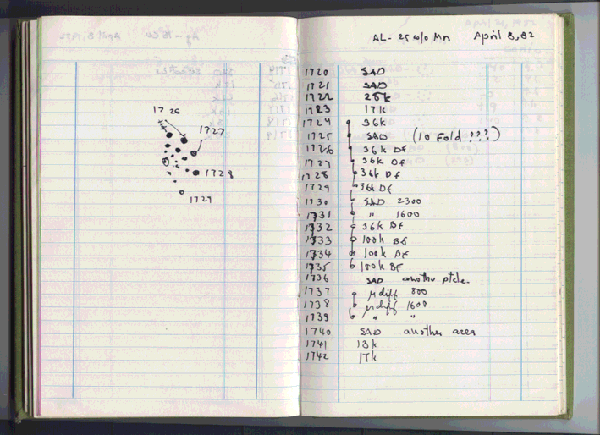

The page in Dan Shechtman's notebook noting his 1982 discovery of a quasicrystal

The page in Dan Shechtman's laboratory notebook noting his April 8, 1982, discovery of a quasicrystal. Whenever you see multiple exclamation points in a scientist's laboratory notebook, it's either very good news, or some equipment problem. (Via Iowa State University).

Shechtman's discovery involved an alloy of aluminum that contained fourteen atomic percent manganese .[8] The alloy was prepared by rapid solidification , a technique that inhibits motion of atoms as the material solidifies. What Shechtman found using electron diffraction was concentric diffraction circles of ten equally-spaced dots; that is, the material exhibited ten-fold rotational symmetry .[6-7]

The spots were as sharp as for any crystal, but the diffraction indicated an icosahedral point group symmetry . This meant that the lattice was not uniform under translation, and the diffraction couldn't be indexed to any Bravais lattice .[8] Crystallography forbids 5-fold (and 10-fold) symmetry.

There was some background to the discovery. Johannes Kepler , who was forever searching for order in the universe , presented quasicrystal-like patterns in his book Mysterium Cosmographicum .[4] More recently, the mathematical physicist , Roger Penrose , created aperiodic tiling patterns (see figure).[4] Penrose asked Shechtman if these tilings had any influence on his work. Shechtman responded that, although he knew about them, they didn't come to mind during the time of his discovery.[4]

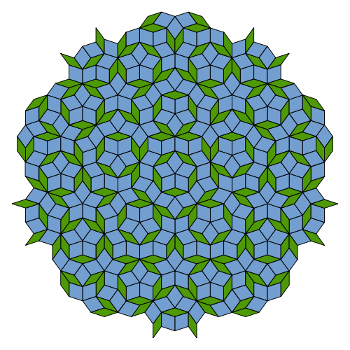A Penrose tiling (P3) using thick and thin rhombi. The symmetry is five-fold, and the structure is aperiodic.

(Via Wikimedia Commons).

One curious thing about quasicrystals is the fact that the ratio of various distances between atoms involves the golden mean .[1] Aside from that tantalizing clue, it's not known why atoms will arrange themselves into quasicrystalline structures. The structures, however, do exhibit some unusual properties, probably because the contained electrons are confused. Actually, the scientific term would be "frustrated ." These attributes might apply only to anthropomorphic electrons.

Quasicrystals formed from metals are non-metallic. They are poor thermal and electrical conductors , their surfaces exhibit low friction , they don't oxidize , and they are hard .[3-4] These useful properties might not be obtained in practical applications, since these materials are metastable ; that is, they will revert to a normal crystalline form when heated.

This was paradigm -busting work, so much so that in 1992 the International Union of Crystallography changed its definition of a crystal from "a regularly ordered, repeating three-dimensional pattern" to a solid with a "discrete diffraction diagram."[2]

The 2011 Nobel Prize in Chemistry

References: